|
|
|
|
|
|
|
|
|
|
|
Vertiefende Informationen zur Sache und Mathematik bezogen auf die Sachsituation:
"Saisonarbeit: Apfelernte in Südtirol" |
|
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
Vertiefende Informationen |
|
|
|
|
|
|
|
|
|
Vertiefende Informationen zu Sache |
|
|
|
Insbesondere wird verwiesen: |
|
|
|
|
|
Der Preis
ist eine abgeleitete Größe |
|
Häufig wird in der Umgangssprache vom Preis 3€ oder 10,99€ gesprochen. Dies ist aber die Währung in der bezahlt wird. Der Preis ist eine abgleitete Größe aus Währung pro Menge: 3€ pro 1kg oder 3,99€ pro Bündel usw. |
|
|
|
|
|
|
|
|
Vertiefende Informationen zur Mathematik |
|
|
|
Mögliche lokale Ordnungen
im Kontext
dieserSachsituation |
|
Die Einstiegsseiten in die fünf lokalen Ordnungs-Bereiche zeigen, welche mathematischen Inhalte durch lokale Ordnung in den Klassen 3 bis 6 (7) eingeführt, geübt und vertieft werden können.
Und: Auf diesen Einstiegsseiten sind gegebenenfalls auch Vertiefungs- möglichkeiten für Lehrpersonen zu finden.
Im Kontext dieser Sachsituation bieten sich lokale Ordnungen zu mathematischen Inhalten in folgenden Bereichen an: |
|
|
|
|
|
|
| |
|
Die Materialien bieten u.a. Hilfen zur Erklärung der Operationen, zu den Algorithmen sowie zum schließenden Rechnen (Zwei- und Dreisatz). Die Materialien bieten Hilfen zur Festlegung von Gewicht, zum Messen von Gewichten, zur Festlegung und Berechnung von Preis, Kosten, Erlös, Gewinn und Lohn sowie zum Umrechnen in andere Maßeinheiten ... |
| |
|
|
| |
|
|
| |
|
Die Materialien bieten Hilfen zur Festlegung von Gewicht, zum Messen von Gewichten, zur Festlegung und Berechnung von Preis, Kosten, Erlös, Gewinn und Lohn sowie zum Umrechnen in andere Maßeinheiten ... |
| |
|
|
| |
|
|
| |
|
Die Materialien bieten Hilfen, um funktionale Abhängigkeiten grafisch darzustellen und ggf. Rechenvorschriften (Terme), die dahinter stecken, mit Excel experimentell zu erarbeiten. |
| |
|
|
| |
|
Die Materialien zu "Fragebögen ..." bieten Hilfen an, um Fragebögen zu gestalten und Zusammenhänge in Datenbeständen zu entdecken. |
| |
|
|
| |
|
Vorwärts-und Rückwärtskalkulation
am Beispiel eines Lebensmittel-Einzelhändlers |
| |
|
|
Vorwärtskalkulation
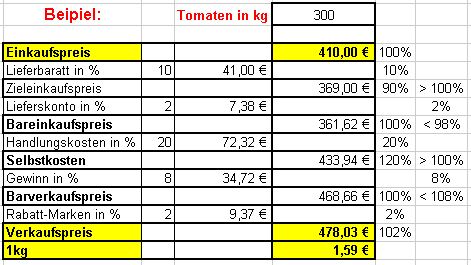
Der Einzelhändler kauft z.B. seine Ware bei einem Großhändler oder direkt bei einem Bauer. Er kalkuliert seinen Verkaufspreis unter den nebenstehenden Bedingungen.
| |
|
| |
|
|
Wie wird gerechnet bzw. programmiert? |
|
Zunächst wird die Menge 300 kg und der Einkaufspreis 410 € eingegeben. Sodann errechnet sich der Lieferrabatt durch 10% von 410 €. Dieser Rabatt wird vom Einkaufspreis subtrahiert. Man erhält den Zieleinkaufspreis, der gegenüber dem Einkaufspreis nur noch 90% beträgt. Setzt man nun den Zieleinkaufspreis wieder gleich 100%, so lässt sich wie zuvor der Bareinkaufspreis berechnen, den man wieder gleich 100% setzt. Nun werden die Handlungskosten mit 20% von 361,62€ berechnet und zum Bareinkaufspreis addiert. Man erhält so die Selbstkosten, die jetzt 120% betragen. Für die folgende Rechnung werden sie wieder gleich 100% gesetzt. usw. usw. Schließlich erhält man den Verkaufspreis für 1kg Tomaten mit 1,59€. |
| |
|
|
| |
|
In der Lern- und Arbeitsumgebung "Modellieren mit Mathe" steht diese Kalkulation als Excelmappe zur Verfügung. Sie ist dort eingebettet in die Modellierung der realen Situation "Transfaire Preise". |
| |
|
|
| |
|
|
Rückwärtskalkulation
Der Einzelhändler will z.B. seine Tomaten (aus Gründen der Konkurrenz) zu einem ganz bestimmten Preis verkaufen und kalkuliert daher, wieviel er dem Großhändler oder Bauern zahlen kann.
|
|
 |
| |
|
|
| |
|
Die Excel-Tabelle sieht äußerlich wie die vorherige aus. Aber sie ist jetzt von unten nach oben (also rückwärts) programmiert worden. |
| |
|
|
Wie wird gerechnet bzw. programmiert? |
|
Zunächst werden der Preis 1,59€ / 1kg und die Menge 300 kg eingegeben. Sodann wird der Verkaufspreis für 300 kg berrechnet. Dieser Verkaufspreis ist 102%, bei der Annahme von Rabattmarken in Höhe von 2%. Der Rabatt errechnet sich mit 477€ · 2 / 102. Er wird vom Verkaufspreis subtrahiert und man erhält den Barverkaufspreis. Analog errechnet sich der Gewinn mit 467,65€ · 8 / 108 und die Selbstkosten wieder durch Subtraktion. usw. usw. Schließlich erhält man den Einkaufspreis von 409,11€ beim Großhändler. Der Unterschied zu 410€ in der ersten Tabelle erklärt sich mit den automatisch vollzogenen Auf- bzw. Abrundungen in den Rechnungen. |
|
|
|
|
|
|
|
|
 |
|
Letzte Änderung: 06.10.2009
© Pädagogisches Institut für die deutsche Sprachgruppe
- Bozen. 2000 -
|
|
|










