|
Definition: Diejenigen x-Werte, bei denen eine Parabel die x-Achse schneidet, heißen Nullstellen der Parabel.
Eine Parabel kann maximal zwei Nullstellen besitzen. Trotzdem kann sie auch eine oder keine Nullstellen haben. Die Anzahl der Nullstellen hängt von der Lage und der Öffnung der Parabel ab. | Zwei Nullstellen: Die Parabel schneidet die x-Achse in 2 Stellen. | 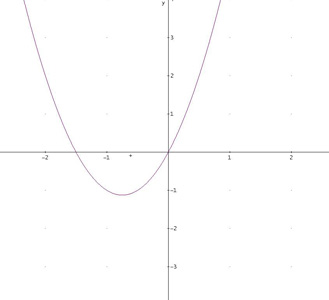 | | Eine Nullstelle: Die Parabel berührt die x-Achse in 1 Stelle. Die Parabel hat eine Nullstelle, wenn das Ergebnis der Diskriminante (b²- 4ac) in der Mitternachtsformel 0 beträgt. | 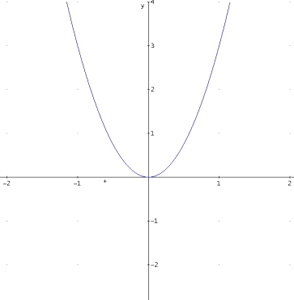 | | Keine Nullstelle: Die Parabel schneidet nicht die x-Achse. Die Parabel hat keine Nullstellen, wenn das Ergebnis der Diskriminante (b²- 4ac) in der Mitternachtsformel negativ ist. | 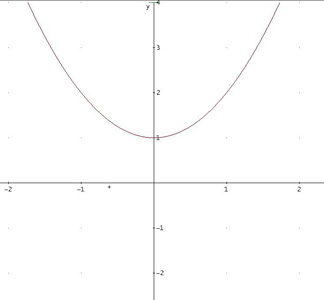 | Beispiel zum Berechnen der Nullstellen © Nicoló
|












