Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen 9 bis 12 |
| |
|
|
| Hinweis:
Die Bearbeitung der Aufgaben zur "Konstruktion und Simulation" können Teil einer Gesamtlösung von arbeitsteilig arbeitenden Kleingruppen sein.
Beschreibung der erwerbaren mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben | |
Die folgenden Lösungen bzw. Ideen zur Konstruktion und Simulation
können Teil einer Gesamtlösung sein (bei der ggf. weitere Kleingruppen parallel an einer Analyse zu Zusammenhängen von Körpergröße und -gewicht arbeiteten.
Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam auch über den Sinn und Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Lösungen und deren Formulierung sind etwa 4 bis 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 2 Schulstunden notwendig. |
| |
|
|
|
|
|
|
|
Konstruktion und Simulation
des Energiehaushaltes eines menschlichen Körpers |
| |
|
|
Konstruiert unter Nutzung der gegebenen Zahlen ein dynamisches Modell für den Energiehaushalt eines menschlichen Körpers.
Beschreibt das Modell zunächst mit Worten und dann in einem Wirkungsdiagramm.
|
|
Jeder Mensch nimmt Energie in Form von Nahrung (potentielle Energie) auf. Diese Energie wird im Körper gespeichert oder in Form eines Grundumsatzes, eines nahrungsabhängigen Umsatzes und eines Arbeitsumsatzes wieder umgewandelt. Grundumsatz und nahrungsabhängiger Umsatz sind individuelle Größen. Der Arbeitsumsatz kann durch körperliche Arbeit oder Sport gesteigert werden. Ein einfaches in- und output Wirkungsdiagramm kann wie folgt aussehen:
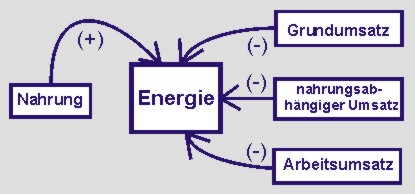
Die Aufnahme von Nahrung wirkt positiv auf die im Körper verfügbare Energie. Grundumsatz, nahrungsabhängiger Verbrauch und Arbeitsumsatz wirken negativ auf diese "eingeführte" Energie. Wir haben es mit der qualitativen Beschreibung eines einfachen In/output-Systems zu tun. |
|
|
|
| Übertragt das Wirkungsdiagramm in ein Flussdiagramm. |
|
Die Zustandsgröße ist die dem Körper konstant zugeführte Energie (E). Nahrungsaufnahme (Z_A), Grundumsatz (A_G), nahrungsabhängiger Umsatz (A_N) und Arbeitsumsatz (A_A) sind Flussgrößen. Auf sie wirken Parameter (rg, rn und ra) für die Energie-Umsätze. Für sie wird zunächst angenommen, dass sie als Summe 100% ergeben. Die Nahrungsaufnahme wird als eine Konstante (ka) angenommen. Ein Flussdiagramm kann dann wie folgt aussehen:
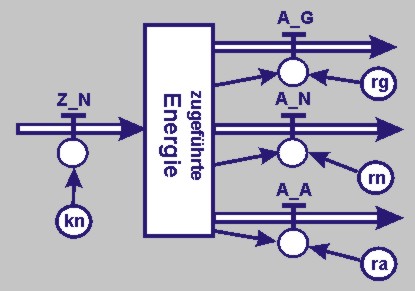
|
|
|
|
| Erstellt die Zustands- und Modellgleichungen. |
|
Die Zustands- und Modellgleichung lassen sich aus dem Flussdiagramm unter Berücksichtigung eines Zeittaktes erschließen. Alle Größen werden mit Zahlen belegt. Das Modell ist nun vollends quantifiziert.
E_neu <-- Δt · (Z_N - A_G - A_N -A_A);
Δt = 1; (Interpretation 1 Tag
E_alt = Z_N = kn; kn = 2000 kcal (pro Tag)
A_G = E · rg; rg = 0,5
A_N = E · rn; rn = 0,1
A_A = E · ra; ra = 0,4
Anmerkung: Die Zahlen für die Raten siehe Seite ma0676.htm#Energieumsatz. |
|
|
|
| Programmiert das Modell mit Excel und simuliert es. |
|
Wir programmieren und simulieren das Modell mit Excel. In der Excel-Tabelle lässt sich die Anfangsgröße für die zugeführte Energie und lassen sich die Raten verändern. Lediglich die Summe der Raten wird zunächst mit 1 angenommen. Geschieht dies, so ergibt sich immer wieder dasselbe Simulationsergebnis.
Siehe hierzu:
ExcelDateien/Mappe1678a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1678a.xls (herunterladbar und interaktiv)
Anmerkung: Zur Programmierung siehe: Crash-Kurse: Einführung in die Nutzung von Excel |
|
|
|
Beschreibt das Verhalten, den Zweck und die Grenzen des Modells.
Simuliert eure erweiterten Modelle
a) für unterschiedliche Essgewohnheiten und
b) für unterschiedliche Sportarten.
|
|
Es gibt keine Zunahme für die Energie. Sie bleibt konstant Null. Die aufgenommene Energie wird stets abgeführt (umgesetzt).
Dieses Modell stimmt sogar für viele Menschen. Sie haben ein konstantes Körpergewicht und nehmen weder zu noch ab. Und diese Modellierung kann der Zweck des Modells sein.
Was geschieht aber, wenn die aufgenommene Energie nicht vollständig umgesetzt wird (ra = 0,3) oder der Arbeitsumsatz durch Sport heftig steigt (ra = 0,5) ? Diese Fragen überschreiten dieses einfache in/output Modell, lassen sich aber mit einfachen Erweiterungen an diesem Modell beschreiben.
Siehe hierzu:
ExcelDateien/Mappe1678b.htm (nur zur Ansicht) oder ExcelDateien/Mappe1678b.xls (herunterladbar und interaktiv)
Siehe hierzu:
ExcelDateien/Mappe1678c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1678c.xls (herunterladbar und interaktiv)
Insbesondere interessiert der Fall, dass "Fressen" und "Hungern" immer wieder aufeinander folgen oder sich nach einer Diät ein schrecklicher Heißhunger einstellt. |
|
|
|
|
|
Ideen zur Konstruktion und Simulation
eines dynamischen Modells
zum Jojo-Effekt |
| |
|
|
| Beschreibt das Modell Jojo-Effekt zunächst mit Worten und dann in einem Wirkungsdiagramm.
|
|
Gibt es ein Energiedefizit so sinkt das Körpergewicht. Nimmt das Körpergewicht zu, so ist eine größere Energiezufuhr notwendig. Das sind die Wechselwirkungen zwischen den Größen Energie und Gewicht.
Grundumsatz, nahrungsabhängiger Umsatz und Arbeitsumsatz werden in diesm Fall zu einer Flussgröße Energieumwandlung zusammengefasst.
Für das Grundmodell "Jojo-Effekt" kann als Ausgangsstruktur das Modell von Räuber und Beute angenommen werden. Es muss aber experimentierend auf das Auf und Ab von Gewichtzunahme und -abnahme angepasst werden. |
| |
|
|
| |
|
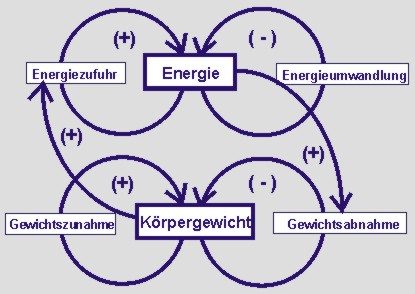 |
|
|
|
| Übertragt das Wirkungsdiagramm in ein Flussdiagramm. Beschreibt sodann das Modell durch Zustands- und weitere Modellgleichungen, programmiert sie und simuliert das Modell. |
|
Anmerkung: Das Modell wird hier nicht weiter ausgeführt. Es wird verwiesen auf die Konstruktion und Simulation
|
|
|
|
| Beschreibt sodann das Systemverhalten, den Zweck und die Grenzen des betrachteten Modells. |
|
|
| |
|
|
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |















