Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung
bezogen auf die Klassen 10 bis 12 |
| |
|
|
Hinweise:
Die Bearbeitung der folgenden Aufgaben kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Kleingruppen sein.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgenden Lösungen zur
können in Teilgruppen der Klasse erarbeitet werden. Sie können aber auch Teil einer Gesamtlösung sein, bei der andere Gruppen der Klasse parallel an weiteren Modellierungen zum Problem "Wachstum, Wachstum über alles" arbeiten. Nach der Präsentation der Gruppenlösungen in der Klasse werden gemeinsam Folgerungen erarbeitet und diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 Schulstunden notwendig, wenn Teile dieser Arbeiten auch als Hausarbeit angefertigt werden. Für die Besprechung aller Analysen in der Klasse sind dann noch einmal ca. 2 Schulstunden notwendig. |
| |
|
|
|
|
|
|
|
Konstruktion und Simulationen
zum dynamischen Wachstum des Kapitals |
| |
|
|
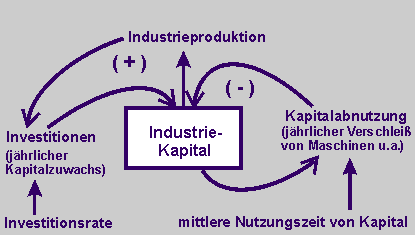
| Diskutiert miteinander und begründet, wie das Industriekapital wächst und zeichnet dazu ein Wirkungsdiagramm. |
|
 |
| |
|
|
| |
|
Mit einem bestimmten Grundstock an aktivem industriellem Kapital (wie Fabrikanlagen, Werkzeugmaschinen, Fahrzeugen) lässt sich jährlich eine bestimmte Menge an Industriegütern erzeugen. Wir gehen davon aus, dass Rohmaterial und Arbeitskraft in ausreichendem Maße vorhanden sind, dann beschränkt nur das Gesamtkapital die Produktionsmenge. ... Ein Teil der industriellen Jahresproduktion stellt aber selbst Industriekapital dar, wie Webstühle, Stahlwerke und Drehbänke, so genannte Industriegüter, die im Endeffekt das Industriekapital vergrößern. (S 30f)
Die Industriegüterproduktion bewirkt einen positiven Regelkreis: Größeres Kapital bewirkt eine höhere Produktion; ein Teil (Bruchteil) der Produktion wird zur Investition, und höhere Investition bedeutet mehr Kapital.
Das Kapital in Form von Investitionsgütern - nur in dieser Form ist Kapital produktionswirksam - nutzt sich ab und wird dann ausgeschieden, z.B. als Schrott. Deshalb gehört zu dem Modell auch ein negativer Regelkreis, der die Kapitalabnutzung berücksichtigt. Die jährliche Kapitalabnutzung wird umso größer, je höher die eingesetzte Kapitalmenge ist. (S 30f) |
| |
|
|
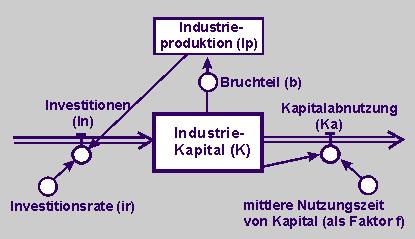
| Beschreibt die Dynamik in einem Flussdiagramm. |
|
 |
| |
|
|
| Erstellt die Zustands- und Modellgleichungen und programmiert sie in Excel |
|
K_neu <-- K_alt + Δt · (In - Ka)
Anfangsgröße Kapital K = 10 Billionen €; Δt = 1; ( 1 Zeittakt = 1 Jahr)
In = Ip · ir Λ Ip = K · b Λ Ka = K · f
ir = 0,2 Λ b = 0,4 Λ f = 0,02 |
| |
|
|
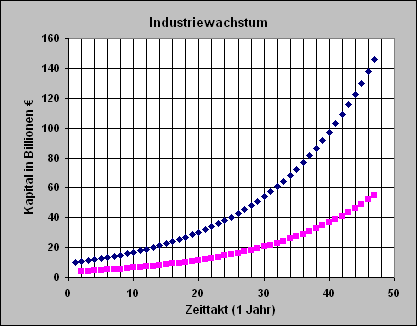
| Simuliert die Dynamik |
|
Siehe hierzu:
ExcelDateien/Mappe1229a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1229a.xls (herunterladbar und interaktiv) |
| |
|
|
| |
|
 |
| |
|
|
|
|
|
|
|
Konstruktion und Simulation
dynamischer Wechselwirkungen
zwischen
Konsum und
Investition |
| |
|
|
| Diskutiert miteinander und begründet, wie Konsum (Kauf-Verhalten) und Investition (Kapitaleinsatz) miteinander wechselwirken können. |
|
Wir nehmen an, dass der Konsum zunimmt und zwar formal genauso, wie auch eine Population (siehe Seite ma1918.htm) wächst. Dieselbe Annahme gilt auch für die Investitionen.
Aber Konsum und Investition wechselwirken aufeinander. (Hierzu siehe Seite ma1919.htm). Dazu nehmen wir an:
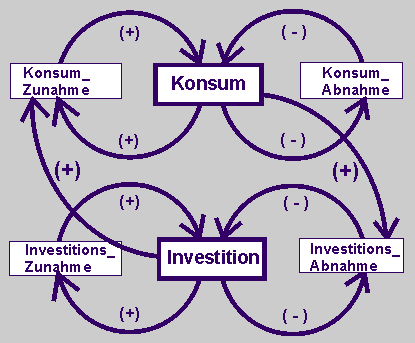
Höhere Investitionen, also ein höherer Kapitaleinsatz, wirken auf den Konsum positiv. Je größer die Investitionen sind, desto mehr wird konsumiert. Umgekehrt wirkt aber ein höherer Konsum auch verstärkend auf die Investitions_Abnahme. Je größer der Konsum wird, desto weniger wird investiert.
Diese qualitative Beschreibung der Wechselwirkungen führt zu dem folgenden Wirkungsdiagramm. |
| |
|
|
| Beschreibt die Wechselwirkungen in einem Wirkungsdiagramm. |
|
 |
|
|
|
| Überlegt euch mögliche Zustandsgrößen, Flussgrößen und Parameter. |
|
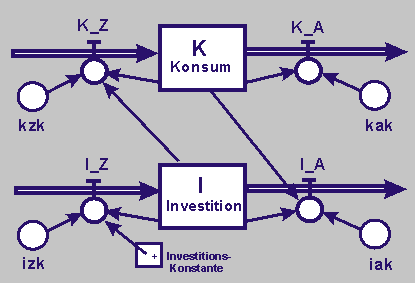
Bei der Übertragung des Wirkungsdiagramms in ein Flussdiagramm haben wir zur Quantifizierung zunächst die beiden Zustandsgrößen Konsum (K) und Investition (I) sowie die vier Flussgrößen Konsum_Zunahme (K_Z), Konsum_Abnahme (K_A), Investitions_Zunahme (I_Z) und Investitions_Abnahme (I_A).
Auf die Zunahme und Abnahme von Konsum und Investition wirkt jeweils ein Koeffizient. Es sind der Konsum_Zunahme_Koeffizient (kzk), der Konsum_Abnahme_Koeffizient (kak), der Institions_Zunahme_Koeffizient (izk) und der Investitions_Abnahme_Koeffizient (iak). Diese Konstruktionen sind strukturell dieselben, wie die Geburten- und Sterberaten beim Wachstum einer Population.
Aber Konsum und Investition wirken aufeinander. I wirkt auf Kz und K wirkt auf Ia und zwar jeweils multiplikativ verknüpft mit den jeweiligen Koeffizienten.
Zusätzlich wird angenommen, dass auf die Investitions_Zunahme eine additive Investitionskonstante (ik) wirkt; was bedeuten kann, dass regelmäßig ein gewisser Betrag investiert wird.
Im folgenden Flussdiagramm sind alle wirkenden Größen benannt und somit auch in einem ersten Schritt quantifiziert. |
| |
|
|
| Beschreibt die Wechselwirkungen sodann in einem Flussdiagramm. |
|
|
|
|
|
Beschreibt das Modell mit Zustands- und Modellgleichungen.
|
|
Die folgenden zwei Zustands- und vier weiteren Modellgleichungen entwickeln wir aus dem Flussdiagramm unter Berücksichtigung eines Zeittaktes zwischen Zustand_neu und Zustand_alt. Alle Anfangsgrößen und Koeffizienten belegen wir mit Zahlen.
K_neu <--
K_alt + Δt · (K_Z - K_A);
Anfangsgröße: K = 4 (Mill €), Δt = 0,3
I_neu <--
I_alt + Δt · (I_Z - I_A),
Anfangsgröße: I = 2 (Mill €), Δt = 0,3
K_Z = kzk · K · I; kzk = 0,3;
K_A = kak · K; kak = 0,8;
I_Z = izk · I + ik; izk = 0,8; ik = 1,5
I_A = iak · I · K; iak = 0,6; |
| |
|
|
| Programmiert das Modell mit Excel. |
|
Die beiden Zustandsgleichungen und die vier weiteren Modellgleichungen programmieren wir, mit den vorgegebenen Größen, in einer Excel-Tabelle. Der rechnerische Zeittakt entspricht dem Δt; er muss interpretiert werden mit etwa 1 Woche oder 1 Monat oder 1 Quartal. Die berechneten Werte in der Tabell sind aber auf vier Stellen hinter dem Komma gerundet.
Siehe hierzu:
ExcelDateien/Mappe1228a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1228a.xls (herunterladbar und interaktiv)
|
|
|
|
| Simuliert das Modell. |
|
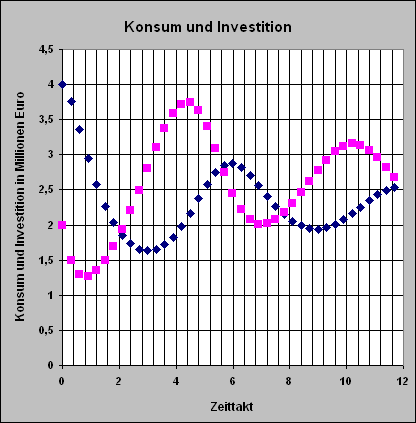
Das folgende Simulationsergebnis entspricht den eingegebenen Größen. Weitere Simulationsergebnisse lassen sich durch Veränderung von Delta t , der Anfangsgrößen, der Koeffizienten und der Konstante erzeugen. |
| |
|
|
| |
|
 |
| |
|
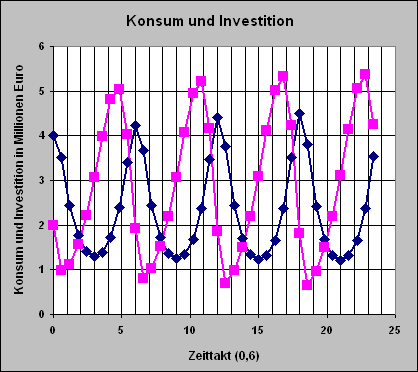
(blaue Rauten = Konsum; violette Quadrate = Investition)
|
| |
|
|
Erste mathematische Reflexion zum Zeittakt und zu Δt |
|
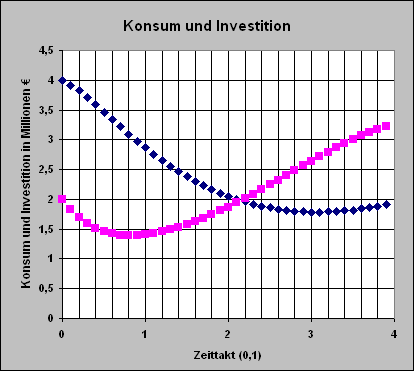
Wird Δt = 0,1 gesetzt, dann ändert sich auch der Zeittakt. Wird aber die Zeittakt-Skala von vorher und werden alle anderen Werte von vorher beibehalten, dann wird nur ein Ausschnitt aus dem vorherigen Diagramm gezeigt.
Siehe hierzu:
ExcelDateien/Mappe1228c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1228c.xls (herunterladbar und interaktiv) |
| |
|
|
| |
|
 |
| |
|
|
Zweite mathematische Reflexion zum Zeittakt und zu Δt |
|
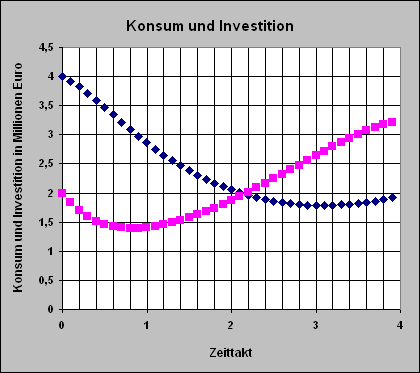
Wird Δt = 0,1 gesetzt, dann ändert sich auch der Zeittakt. Wird nun die Zeittakt-Skala den neuen rechnerischen Zeitschritten angepasst und werden alle anderen Werte von vorher beibehalten, dann wird das zuvor dargestellte Diagramm auf die neue Eichung der Zeittakt-Achse gestreckt.
Siehe hierzu:
ExcelDateien/Mappe1228f.htm (nur zur Ansicht) oder ExcelDateien/Mappe1228f.xls (herunterladbar und interaktiv) |
| |
|
|
|
|
 |
| |
|
|
Dritte mathematische Reflexion zum Zeittakt und zu Δt |
|
Eine Vergrößerung von Δt = 0,6 ändert den Zeittakt erneut. Wird die Zeittakt-Skala diesen neuen rechnerischen Zeitschritten angepasst und werden alle anderen Werte von vorher beibehalten, so ergibt sich das folgende Diagramm. Im Vergleich zum ersten zeigt es aber ein anderes Verhalten. Mit Vergrößerung von Δt wird also eine Interpretation immer schwieriger bis kaum noch sinnvoll.
Siehe hierzu:
ExcelDateien/Mappe1228g.htm (nur zur Ansicht) oder ExcelDateien/Mappe1228g.xls (herunterladbar und interaktiv) |
| |
|
|
|
|
 |
|
|
|
| Beschreibt das Systemverhalten und interpretiert es.
Diskutiert miteinander den Zweck und die Grenzen der Modells. |
|
Konsum und Investition schwingen zeitversetzt und gegenläufig. Nimmt der Konsum ab, so steigen die Investitionen. Nimmt der Konsum wieder zu, so fallen die Investitionen. Und das immer ein wenig zeitlich nachhinkend. Dieselbe Erkenntnis lässt sich auch aus den Simulationen gewinnen, in denen die Werte für die Anfangsgrößen, die Koeffizienten und für die Konstante nicht zu stark abgewandelt worden sind.
Der Zweck des Modells kann also genau diese qualitative Erkenntnis sein: Konsum und Investition schwingen zeitversetzt und gegenläufig immer zeitlich etwas nachhinkend.
Soll der Zweck des Modells eine quantitative Vorhersage sein, so müssen die Anfangsgrößen, die Koeffizienten und die Konstante aus den aktuellen Wirtschaftsdaten (siehe hierzu z.B. die Seite ma0224.htm#Heute) heraus analysiert werden.
Die Grenzen dieses Modells liegen aber immer in den Annahmen, die in dem Flussdiagramm zu sehen sind. Denkbar wären auch andere Wechselwirkungs-Kopplungen zwischen Konsum und Investition. Und es gibt auch einen Zusammenhang von Konsum und Investition mit dem Volkseinkommen. |
|
|
|
|
|
Konstruktion und Simulation dynamischer Wechselwirkungen
zwischen Volkseinkommen, Konsum und Investition |
| |
|
|
| Diskutiert miteinander und begründet, welche (qualitative) Bedeutung das Kauf-Verhalten (Konsum) der Bevölkerung und das eingesetzte Kapital (Investition) auf das Volkseinkommen haben.
Beschreibt qualitativ die Wechselwirkungen. |
|
In diesem Modell wird der Wechselwirkungszusammenhang zwischen Konsum und Investition beibehalten, so wie er oben im Flussdiagramm dargestellt ist. Zusätzlich wird jetzt aber die Zustandsgröße Volksvermögen (V) und die Flussgröße Summe (Su) eingefügt.
Als kompetente Laien nehmen wir an, dass der Wechselwirkungszusammenhang von Konsum und Investition wie folgt qualitativ auf das Volkseinkommen wirkt:
Wird mehr konsumiert, so steigt das Volkseinkommen z.B. über die Mehrwertsteuer. Also: Die Konsum_Zunahme wirkt positiv auf die Flussgröße "Summe".
Wird aber weniger konsumiert, nimmt also der Konsum ab, so wird gespart und das Volkseinkommen steigt ebenfalls. Also: Die Konsum_Abnahme wirkt ebenfalls positiv auf die Flussgröße "Summe".
Wird aber weniger investiert, nimmt also die Investition ab, so sinkt auch das Volksvermögen. Also: Die Investitions_Abnahme wirkt negativ auf die Flussgröße "Summe".
Schließlich nehmen wir einen Summen_Anpassungsfaktor ( saf ) an, der auf die Flussgröße Summe wirkt.
Das Volksvermögen steigt also über die Flussgröße Summe an. Letztere wirkt daher, wie eine Investitionskonstante, additiv auf die Investitions_zunahme.
|
| |
|
|
| |
|
Eine ökonomisch ausführliche Beschreibung zu diesem Modell ist unter http://de.wikipedia.org/wiki/Multiplikator-Akzelerator-Modell zu finden. Hierfür sind wirtschaftliche Grundkenntnisse notwendig, die einem kompetenten Laien aber nicht mehr ohne weiteres verfügbar sind. |
| |
|
|
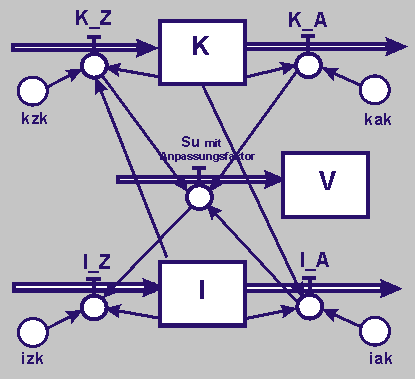
| Beschreibt die Wechselwirkungen in einem Flussdiagramm, in dem das Volkseinkommen in Abhängigkeit von Konsum und Investition dargestellt wird.
Überlegt euch zu diesem Zweck die Zustandsgrößen, mögliche Flussgrößen und Parameter. |
|
|
| |
|
|
Beschreibt das Modell mit Zustands- und Modellgleichungen.
|
|
Die folgenden drei Zustands- und fünf weiteren Modellgleichungen werden aus dem Flussdiagramm entwickelt unter Berücksichtigung der obigen qualitativen Beschreibung und eines Zeittaktes zwischen Zustand_neu und Zustand_alt. Alle Anfangsgrößen und Koeffizienten belegen wir mit Zahlen.
K_neu <-- K_alt + Δt · (K_Z - K_A);
Anfangsgröße: K = 4 (Mill €),
Δt =0,1
I_neu <-- I_alt + Δt · (I_Z - I_A),
Anfangsgröße: I = 2 (Mill €),
V_neu <-- V_alt + Su,
Anfangsgröße: V = 0 (Mill €),
K_Z = kzk · K · I; kzk = 0,3;
K_A = K · kak; kak = 0,8;
Su = (Kz + Ka - Ia) · saf; saf = 0,1
I_Z = izk · I + Su; izk = 0,8;
I_A = iak · I · K;
iak = 0,6;
Die Koeffizienten, die in obigem Wechselwirkungsmodell für Konsum und Investition gewählt wurden, werden hier beibehalten. Lediglich für Δt wird 0,1 gewählt. Das entspricht aber der zweiten oben dargestellten Simulation.
|
| |
|
|
| Programmiert das Modell mit Excel. |
|
Die drei Zustandsgleichungen und die fünf weiteren Modellgleichungen programmieren wir, mit den vorgegebenen Größen, in einer Excel-Tabelle. Der rechnerische Zeittakt entspricht dem Δt; er muss interpretiert werden mit etwa 1 Woche oder 1 Monat oder 1 Quartal. Die berechneten Werte in der Tabelle sind auf vier Stellen hinter dem Komma gerundet.
Siehe hierzu:
ExcelDateien/Mappe1228e.htm (nur zur Ansicht) oder ExcelDateien/Mappe1228e.xls (herunterladbar und interaktiv)
|
| |
|
|
| Simuliert das dynamische Modell. |
|
Das folgende Simulationsergebnis entspricht den eingegebenen Größen.
Weitere Simulationsergebnisse lassen sich durch Veränderung von Delta t, den Anfangsgrößen, den Koeffizienten und der Konstante erzeugen. |
| |
|
|
| |
|
|
| |
|
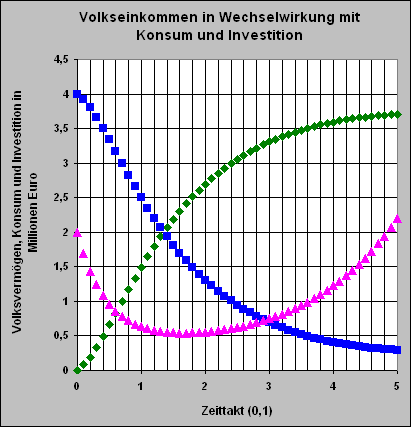
(blaue Quadrate = Konsum; violette Dreiecke = Investition;
grüne Rauten = Volkseinkommen) |
| |
|
|
| Beschreibt das Systemverhalten und interpretiert es.
Diskutiert miteinander, welche Bedeutung die Simulationen für euer Handeln haben kann und wo der Zweck und die Grenzen der Modellierung liegen. |
|
Wir bringen das vorstehende Simulationsergebnis mit dem zweiten oben dargestellten Simulationsergebnis für Konsum und Investition in Verbindung. Dann können wir zunächst wieder feststellen, dass der Konsum und die Investition zeitlich versetzt hintereinander herhinken. Hier aber etwas deutlicher, als oben für Konsum und Investition.
Das Volksvermögen steigt erst schneller dann immer langsamer, je nachhaltiger der Konsum nachlässt.
Das Volksvermögen nähert sich sogar einem Höchstwert und sinkt dann wieder, wie das folgende Simulationsergebnis zeigt, in dem Δt und saf verdoppelt wurden. Das Volksvermögen bildet träge Wellen aus, die sich dem zeitlich versetzten Schwingen von Konsum und Investition überlagern.
Siehe hierzu auch:
ExcelDateien/Mappe1228d.htm (nur zur Ansicht) oder ExcelDateien/Mappe1228d.xls (herunterladbar und interaktiv)
Der Zweck des Modells kann also für ökonomische Laien genau diese grobe qualitative Erkenntnis sein. Oder noch einfacher: Ein gesteigerter Konsum wirkt sich positiv auf das Volkseinkommen aus. Konsum ist am Wirtschaftswachstum beteiligt.
Natürlich steckt in dieser letzten Feststellung auch eine Hoffnung. Denn langfristig wird nur dann ein Wachstum des Volkseinkommens (des BIP) möglich sein, wenn auch noch viele andere Faktoren zur Wirkung kommen.
Diese letzte Feststellung sagt dann aber auch, dass die vorstehende Modellierung ihr Grenzen hat und nur mit ökonomischen Grundkenntnissen erweiterbar ist. |
| |
|
|
| Verschriftlicht eure Ergebnisse und erstellt eine Präsentation. |
|
Wesentliche Ergebnisse sind in den ExcelMappen dargestellt. Die Interpretationen sind im vorstehenden Text zu finden. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |























