Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen 10 bis 12 |
| |
|
|
Hinweise:
Die Bearbeitung der Aufgaben zur "Konstruktion und Simulation von dynamischen Wechselwirkungen" kann Teil einer Gesamtlösung von arbeitsteilig arbeitenden Gruppen sein.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgende Lösung zur Konstruktion und Simulation der dynamischen Wechselwirkungen zwischen Spinnmilben und Raubmilben kann in Teilgruppen der Klasse erarbeitet werden.
Sie können Teil einer Gesamtlösung sein, bei der etwa drei weitere Kleingruppen parallel an Wachstumsmodellen für Spinnmilben (oder Raubmilben) arbeiten.
Nach der Präsentation aller Gruppenlösungen in der Klasse wird gemeinsam der Zweck von dynamischen Wachstumsmodellen und insbesondere auch von Räuber-Beute-Modellen diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 - 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 1 - 2 Schulstunden notwendig.
|
| |
|
|
|
|
|
|
|
Modell zu dynamischen Wechselwirkungen
zwischen Spinnmilben und Raubmilben |
| |
|
|
| Konstruiert ein so genanntes Räuber-Beute-Modell, das die dynamischen Wechselwirkungen zwischen Spinnmilben und Raubmilben beschreibt.
|
|
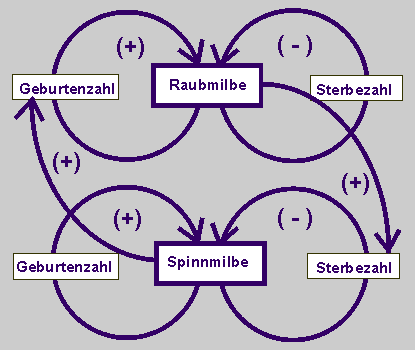
Wir diskutieren miteinander und entscheiden uns, was auf das Wachstum der Raubmilben und was auf das Wachstum der Spinnmilben wirkt. Wie überlegen wie es wirkt, positiv oder negativ? Und wie das Wachstum der Raubmilben und Spinnmilben aufeinander wirkt?
Das folgende Wirkungsdiagramm zeigt zwei Diagramme zum ungebremsten Wachstum, eins für die Raubmilben und eins für die Spinnmilben. Aber diese beiden Diagramme sind miteinander gekoppelt. Die zunehmende Anzahl der Spinnmilben wirkt positiv auf die Geburtenzahl der Raubmilben. Je mehr Nahrung die Raubmilben vorfinden, desto stärker werden sie sich vermehren. Und die Anzahl der Raubmilben wirkt positiv auf die Sterbezahl der Spinnmilben. Denn je mehr Raubmilben leben, desto mehr Spinnmilben werden sterben oder desto größer wird die Sterbezahl der Spinnmilben sein. |
| |
|
|
| Beschreibt eurer Modell zunächst in einem Wirkungsdiagramm. |
|
 |
|
|
|
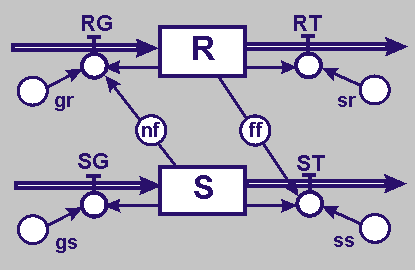
Übertragt das Modell in die Flussdiagrammsymbolik.
Die quantifizierte Beschreibung des Wachstums einer Art mit Geburten- und Sterberate siehe Seite zuvor. |
|
Zur quantifizierten Beschreibung des Wachstums von Spinnmilben und Raubmilben kommen nun die Wirkungen aufeinander hinzu.
Einerseits wirken die Spinnmilben über einen Nahrungsfaktor auf die Raubmilben_Geburten. Der Faktor nf quantifiziert dabei den Anteil der Spinnmilben, die jeweils Nahrung sind.
Andererseits wirken die Raubmilben über einen Fressfakor auf die Spinnmilben_Todesfälle. Der Faktor nf quantifiziert dabei den Anteil von Spinnmilben, der jeweils gefressen wird. |
| |
|
|
Abkürzungen:
S Spinnmilbe; R Raubmilbe;
SG Spinnmilbengeburt;
RG Raubmilbengeburt;
ST Spinnmilbentod;
RT Raubmilbentod,
gs = Geburtenrate Spinnmilben
gr = Geburtenrate Raubmilben;
ss = Sterberate Spinnmilben;
sr = Sterberate Raubmilben;
nf = Nahrungs-Faktor;
ff = Fress-Faktor |
|
 |
|
|
|
Formuliert die Veränderung der Zustandsgrößen durch Zustandsgleichungen und die Veränderung der Flussgrößen durch weitere Modellgleichungen.
|
|
In derselben Weise wie für Spinnmilben (Seite zuvor) bestimmen wir die Geburtenrate der Raubmilben. „Die Lebensdauer erwachsener Raubmilben beträgt ca. 4 Wochen, in dieser Zeit werden pro Weibchen ca. 50 – 100 Eier abgelegt.
Die Sterberate der Raubmilben nehmen wir, wie auch bei den Spinnmilben, als halb so groß an, wie die Geburtenrate. Denn die Raubmilben haben eine Lebenszeit von 4 Wochen.
In den folgenden zwei Zustands- und vier weiteren Modellgleichungen, die sich aus dem Flussdiagramm unter Berücksichtigung eines Zeittaktes zwischen Zustand_neu und Zustand_alt entwickeln lassen, wird das Modell noch einen weiteren Schritt quantifiziert, indem auch die Anfangsgrößen, Raten und Faktoren mit Zahlen belegt werden.
S_neu <-- S_alt + Δt · (SG - ST);
Anfangsgröße: S = 100;
R_neu <-- R_alt + Δt · (RG - RT);
Anfangsgröße: R = 70;
Δt = 0,5; (Interpretation desZeittaktes = 1 Tag)
Zur Notwendigkeit und Bedeutung der Interpretation des Zeittaktes
siehe Seite "Fehler" bei der Modellbildung und Interpretation -
Exkurs in die Analysis“
SG = gs· S; gs = 0,35
ST = ss· S · R · ff; ss = 0,17; ff = 0,01
RG = gr · R · S · nf; gr = 0,22; nf = 0,005
RT = sr · R; sr = 0,11;
|
|
|
|
| Programmiert euer Modell in einer Excel-Tabelle auf der Grundlage aller Modellgleichungen.
|
|
Wir programmieren die Modellgleichungen in einer Excel-Mappe.
Siehe hierzu:
ExcelDateien/Mappe1918f.htm (zur Ansicht) oder ExcelDateien/Mappe1918f.xls (herunterladbar und interaktiv)
ExcelDateien/Mappe1918g.htm (zur Ansicht) oder ExcelDateien/Mappe1918g.xls (herunterladbar und interaktiv)
Zwar könnten wir die Zahlenwerte noch immer schrittweise ausgerechnen, aber der Rechenaufwand wird jetzt sehr hoch. Excel wird für uns notwendige Hilfe.
In den Rechnungen haben wir die Werte für SG, ST, RG und RT auf zwei und die Werte für S und R auf eine Stelle hinter dem Komma gerundet. |
|
|
|
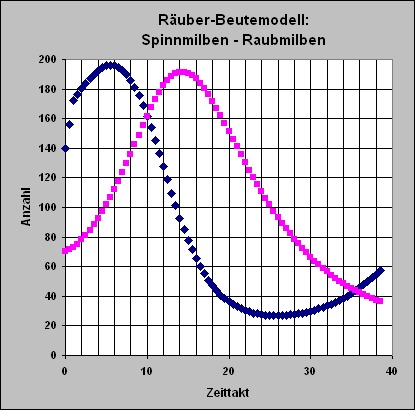
Simuliert euer Modell unter unterschiedlichen Bedingungen, insbesondere unter unterschiedlich starken Kopplungen.
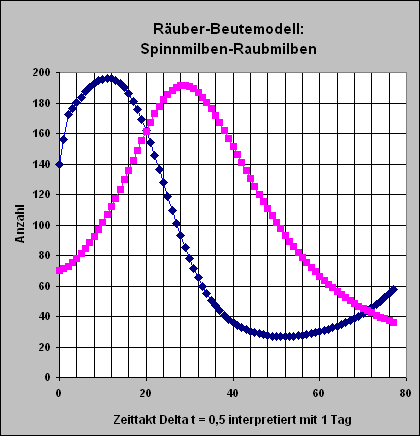
>> Das Diagramm entspricht
den Werten der Tabelle; Delta t ist im Zeittakt geeicht! |
|
 |
| |
|
|
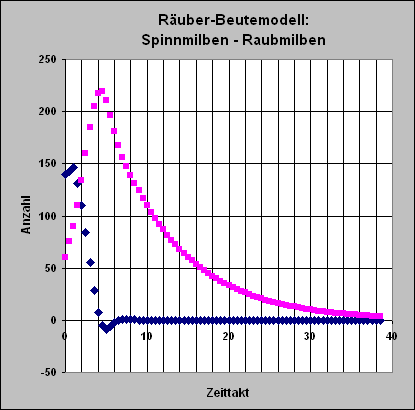
>> Das Diagramm entspricht
den Werten der Tabelle; Delta t ist in Tagen geeicht! |
|
|
| |
|
|
>> In nebenstehenden
Simulation ist
R = 60 und S = 140.
Der Fressfaktor ist ff = 0,03
und der Nahrungsfaktor
ist nf = 0,02.
Letzterer ist radikal
erhöht worden.
Siehe:
ExcelDateien/Mappe1918h.htm (zur Ansicht) oder ExcelDateien/Mappe1918h.xls (herunterladbar und interaktiv)
|
|
|
|
|
|
Diskutiert miteinander, wie sinnvoll und realistisch die Werte für die Parameter sind.
Finden von robusten Werten" |
|
Einige systematisch vorgenommene Simulationen zeigen uns die mathematischen Grenzen des Modells auf. Hierzu zwei Beispiele:
Beispiel 1: Bei Beibehaltung von Delta t und aller Raten und Faktoren in der obigen Tabelle aber mit S=500 und R=100 ist das Simulationsergebnis mathematisch nicht mehr deutbar. Es gibt dann nämlich negative Zahlen für die Spinnmilben. Siehe hierzu auch das letzte Simulationsergebnis. Reduziert man in diesem Fall den Nahrungsfaktor auf nf = 0,001, so ist das Ergebnis zwar wieder mathematisch deutbar aber kaum realistisch für den Plantagenbesitzer. Erhöht man dann zusätzlich den Nahrungsfaktor auf nf=0,007, so liefert die Simulation wieder Unsinn!
Beispiele 2: Änderungen a) an den Anfangsgrößen für Spinn- und Raubmilben sowie b) an den Sterberaten für Spinn- und Raubmilben sowie c) an den Kopplungsfaktoren ff und nf wirken entscheidend auf das Verhalten des Modells ein. Übertreibungen bei diesen Größen führen sehr schnell zu nicht mehr deutbaren Simulationsergebnissen.
Wir können also feststellen:
1. Das Modell ist für Delta t, die Raten, die Faktoren und die Anfangsgrößen nur in gewissen Intervallen mathematisch deutbar. Außerdem sind die Intervallgrenzen auch noch voneinander abhängig. Erhöht man z.B. eine Geburtenrate in extremer Weise, so hat das Einfluss auf fast alle anderen Werte.
2. Für Delta t, die Raten, die Faktoren und die Anfangsgrößen gibt es Zahlen, bei denen das Modell relativ stabile mathematische Deutungen zulässt. Diese sind aber eine notwendige Voraussetzung für eine Interpretation in die Realität. Solche Werte für die Größen, bei denen das Modell relativ stabil reagiert, werden auch als robust bezeichnet. Robuste Werte können mittels abschätzender Berechnung (etwa für die Geburten- und Sterberaten) aber auch mittels Simulationen (etwa für die Anfangsgrößen, Nahrungs- und Fressfaktoren) gefunden werden.
|
|
|
|
| Beschreibt das Systemverhalten und interpretiert die Simulationsergebnisse sowie die Grenzen und den Zweck dieser Modelle z.B. in Bezug auf die Schädlingsbekämpfung und vergleicht es mit der Nutzung von Insektiziden. |
|
Simulationen erlauben eine zeitliche Beschreibung des Verhaltens von Raub- und Spinnmilben zueinander. Mit zunehmender Zahl von Raubmilben wird nach einer gewissen Zeit die Zahl der Spinnmilben, die zunächst noch zunehmen, kleiner. Nimmt aber die Zahl der Spinnmilben ab, so wird auch wieder nach einer gewissen Zeit die Zahl der Raubmilben kleiner. Sinkt sie unter ihre Anfangsgröße, so kann sich die Spinnmilbenpopulation wieder erholen und wächst wieder an. Der Zyklus wiederholt sich ohne Eingriff von Außen.
Ein Wachstums-Modell, das sich wie Raub- und Spinnmilben verhält, nennt man allgemein ein Räuber-Beute-Modell. Diese Art von Wachstum ist in der Ökologie häufig anzutreffen: Zwei Arten verhalten sich in einem dynamischen Gleichgewicht zueinander. Natürlich sind bei anderen Arten, wie bei Fuchs und Hase, die Modellgrößen andere. Aber diese Art des Wachstums wird auch auf andere Wirklichkeitsbereiche übertragen. So beschreibt z.B. Eduard Pestel in seinem Bericht an den Club of Rome (Jenseits der Grenzen des Wachstums, 1988) ökonomisch-gesellschaftliche Wachstumsprozesse mit „Organischem Wachstum“.
Die dynamische Modellierung mit robusten Wachstumsgrößen hat unterschiedliche Zwecke:
Einerseits führen die Simulationen des Modells bereits zur Erkenntnis, wie diffizil Räuber- und Beutepopulationen aufeinander einwirken. Wie kompliziert wird dann erst das Verhältnis in Nahrungsnetzen sein?! So erhalten wir also die folgende qualitative Interpretation: Die Simulationen mit robusten Wachstumsgrößen belegen und begründen den Vorteil einer biologischen Schädlingsbekämpfung, in der weder die eine noch die andere Art völlig ausstirbt. Bei der Behandlung mit Insektiziden würden schließlich beide Arten absterben und das hätte in der freien Natur Folgen für ein empfindliches Nahrungsnetz.
Andererseits können die Simulationen des Modells dabei helfen, in einer Gurken-Plantage, in der sich Spinnmilben ausgebreitet haben, ökologisch sinnvolle Schritte zu gehen. So erhalten wir eine quantitative Interpretation: Nur wenige ausgesetzte Raubmilben (etwa Zweidrittel der Spinnmilben-Population) dezimieren die Spinnmilben in relativ kurzer Zeit. In dem von uns simulierten Fall, in dem die robusten Wachstumsgrößen experimentell oder rechnerisch abgeschätzt worden sind, sind die Spinnmilben nach 50 Tagen nahezu komplett beseitigt. Zwar leben dann sehr viele Raubmilben. Aber sie schaden den Pflanzen nicht. Die Raubmilben sterben dann quasi einen Hungertod. Sie haben keine Nahrung mehr. Würden dann aber nach zwei Monaten (60 Tagen) die Pflanzen nicht geerntet, so würden sich die wenigen Spinnmilben wieder vermehren und der Zyklus neu beginnen. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |