Zunächst eine Erinnerung:
|
|
Ihr habt bei der Arbeit etwa an den realen Problemen "Fahrplan für eine eingleisige Strecke" oder "Handys und Geldsorgen" lineare Abhängigkeiten kennengelernt. |
| |
|
|
Worin unterscheiden sich die beiden Geraden der
Weg/Zeit-Abhängigkeiten?
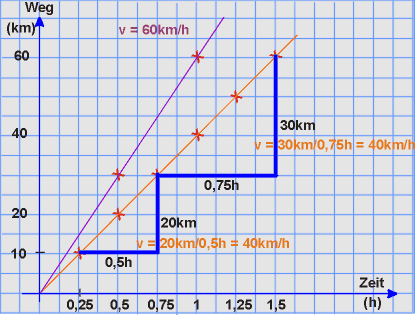
Auffällig ist: die Geraden sind unterschiedlich steil.
Oder anders gesprochen:
Die Geraden haben einen unterschiedlichen Anstieg oder eine unterschiedliche Steigung.
|
|
 |
| |
|
|
Steigung (oder Anstieg)
einer Geraden |
|
Die Gerade bei einer mittleren Geschwindigkeit von 60km/h ist steiler als die bei einer mittleren Geschwindigkeit von 40km/h.
Die Steigung der Geraden bei einer mittleren Geschwindigkeit von 40km/h kann etwa durch die Quotienten (20km : 0,5h) oder (30km : 0,75h) oder (...) angegeben werden. Und: Alle diese Quotienten haben denselben Wert 40km/h. |
| |
|
|
Steigung, Steigungsdreieck |
|
Anders gesprochen: Die Steigung der Weg/Zeit-Gerade für v = 40km/h ist überall gleich. Auf 0,5h nach rechts steigt die Gerade um 20km. Oder auf 0,75h nach rechts steigt die Gerade um 30km. Der Quotient aus dem jeweiligen Weg und der jeweiligen Zeit aller dieser Steigungsdreiecke (blau) ist also immer gleich, nämlich konstant 40km/h. Entsprechend hat die andere Weg/Zeit-Gerade die Steigung 60km/h.
Allgemein: Mittels eines "Steigungsdreiecks" lässt sich die Steigung einer Geraden berechnen. |
| |
|
|
Worin unterscheiden sich
die beiden Geraden der Kosten/Zeit-Abhängigkeit?
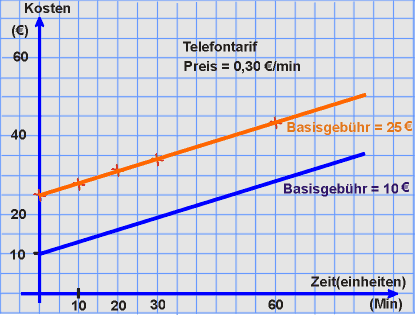
Auffällig ist: Die beiden Geraden haben dieselbe Steigung und verlaufen parallel zueinander. Aber die Schnittpunkte mit vertikalen Achse sind verschieden. |
|
 |
| |
|
|
Abschnitt auf
der vertikalen Achse |
|
Die Gerade mit der Basisgebühr von 25€ schneidet die vertikale Achse im Punkt (0min/25€). Der zweite Paar-Wert bedeutet die Basisgebühr des Telefontarifs.
Viele Geraden - wie die zur Weg/Zeit-Abhängigkeit - gehen durch den Koordinatenurprung (0/0). Sie schneiden die vertikale Achse bei Null. |
| |
|
|
Zunächst:
Eine kurze Zusammenfassung |
|
Die einzelnen Geraden können sich also in zweierlei Hinsicht unterscheiden: Sie haben eine(n) unterschiedliche(n) Steigung (Anstieg) und sie schneiden die vertikale Achse in unterschiedlichen Punkten. |
|
|
|
Nun aber:
Abstraktion von linearen Termen von den konkreten Bedeutungen
Wir abstrahieren von den Größen
(wie Zeit, Preis, Kosten, Tarife, Geschwindigkeit,
...) und
schreiben für die unabhängige Variable die Leerstelle x und für die abhängige Variable die Leerstelle y.
Die waagerechte Achse wird dabei zur x-Achse und die vertikale Achse zur y-Achse. Zusätzlich erweitert sich Koordinatensystem in die negativen Zahlbereiche.
Dann erhalten wir
zur Beschreibung der beiden
Tarif-Geraden die beiden folgenden
abstrakten Formen: | |
 |
| |
|
|
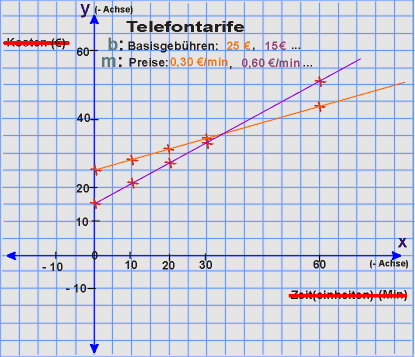
y = 0,30 · x + 25
|
|
Die Punkte auf der roten Geraden erfüllen die nebenstehende Gleichung. Die Wertepaare machen jeweils aus der Aussageform eine wahre Aussage.
x |
0 |
10 |
20 |
30 |
60 |
y |
25 |
28 |
31 |
34 |
42 |
|
| |
|
|
y = 0,60 · x + 15
|
|
Die Punkte auf der lila Geraden erfüllen die nebenstehende Gleichung: Die Wertepaare machen aus der Aussageform eine wahre Aussage.
x |
0 |
10 |
20 |
30 |
60 |
y |
15 |
21 |
27 |
33 |
51 |
|
| |
|
|
Und noch einen weiteren Schritt abstrakter...
erhalten wir ein Funktion mit Formvariablen:
|
|
Auch für die veränderlichen Konstanten (wie Geschwindigkeit und Preis oder Basisgebühr und Startzeiten bei Zügen) für Steigung und Abschnitt auf y-Achse können wir Buchstaben einführen, hier: m und b. Dadurch wird es noch einmal abstrakter und formaler, aber auch allgemeiner. Nutzt man diese allgemeinen und abstrakten Formen in Anwendungssituationen, so muss man sie natürlich wieder mit Inhalt füllen. Man muss sie interpretieren. D.h. die hier vorgenommen abstrakten Schritte müssen wieder rückwärts gegangen werden. |
| |
|
|
y = m · x + b
|
|
Die Variablen m und b nennt man auch Formvariable oder Parameter. Sie sagen etwas über die Form bzw. Lage der Geraden aus.
Natürlich hätte man auch andere Buchstaben nehmen können. Aber die genannten haben sich in der Mathematik eingebürgert und sind in fast allen Schulbüchern so zu finden.
|
| |
|
|
Steigung
und
y-Achsenabschnitt
einer Geraden |
|
Die Formvariable (der Parameter) m gibt die Steigung (oder den Anstieg) der Geraden an.
Die Formvariable (der Parameter) b gibt den Schnittpunkt (0/b) der Geraden mit der y-Achse an. Man sagt zu b auch y-Achsenabschnitt. |
| |
|
|
|
|
|
| |
|
|
Ideen für mögliche, selbstorganisierte
Übungen:

|
|
Ihr kennt die Verkehrsschilder, auf denen die Steilheit einer Straße in Prozenten angegeben wird. Hat eine Straße ein Gefälle von 10% (= 10/100) so bedeutet dies: sie steigt (fällt) auf 100 Metern 10 Meter.
Die Steigung einer Straße kann man auch durch den Winkel angeben der zwischen der Horizontalen und der Straße aufgespannt wird. Eine Steigung von 100% würde dann 45 Grad bedeuten.
- Welche durchschnittliche Steigung hat die Mautstraße "Kolm-Salgurn" von 4,5 km Länge und einem Höhenunterschie von 1230m - 1580m?
- Welche Steilheit hat eine Felswand, die fast senkrecht in die Höhe geht?
- Mit welchem Anstieg heben sich Flugzeuge in den Himmel?
|
| |
|
Um 6 Uhr startet ein Interregio von Aachen nach Hagen. Gleichzeitig startet in Hagen ein Güterzug nach Aachen. Zu welcher Zeit und in welcher Entfernung von Hagen begegnen sich die Züge, wenn die mittleren Geschwindigkeiten 100km/h (Interregio) und 75km/h (Güterzug) betragen?
- Erstelle zur Tabelle einen Graf
- Erstelle zum Graf eine Wertetabelle
- Finde zur Geraden die Funktionsgleichung
- Erstelle zur Funktionsgleichung eine Wertetabelle und zeichne die Gerade.
|
Verweise auf Angebote außerhalb dieser Lernumgebung
|
|
Experimentiert mit den Schiebereglern und Animationen zu den Geradengleichungen auf den interaktiven Seiten des Mathematischen Instituts der Uni Wuppertal.
Auf diesen Seiten gibt es u.a. vier Seiten zu Ursprungsgeraden (Gerade, Steigung...), vier Seiten zu Gleichungen, eine Seite zu Nullstellen und zwei Seiten zu Schnittpunkten. |
| |
|
|
|
|
Das online-Lexikon wikipedia bietet vertiefende Informationen
|








