Würfel und Quader

Zwei Geraden spannen
eine Ebene auf.

Vereinbarungen zu Punkten, Geraden, Strecken und Ebenen

Zwei Ebenen können sich schneiden, dann haben sie eine Schnittgerade. Zwei Ebenen können aber auch parallel zueinander sein.

Quader und Würfel

Ein Schrägbild des Würfels und Quaders

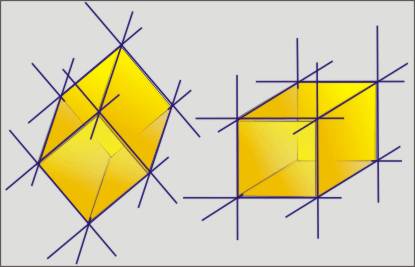
Drei Ebenenpaare, also insgesamt sechs Ebenen (siehe Figur oben), die sich schneiden, formen einen Körper.
Sind die drei Ebenenpaare zu je zweit parallel und stehen sie zu je zweit aufeinander senkrecht, so entsteht ein Quader.
Sind zusätzlich die sechs begrenzten Flächen gleich groß, so haben wir einen Würfel.

Ideen für mögliche, selbstorganisierte
Übungen:

Alle Würfel sind Quader. Gilt auch die umgekehrte Aussage: Alle Quader sind Würfel.?
Zeichnet mit dem Geodreieck Quader und Würfel.
Betrachtet einmal das folgende Bild von Victor Vasarely.
Welche Formen könnt ihr entdecken?
Wie entsteht der räumliche Eindruck?
Versucht selbst einmal, ein Bild ähnlicher Art zu malen.

Victor Vasarely,
Keple-Gestalt, 1968