Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen (9) 10 bis 12 |
| |
|
|
Hinweise:
Die Bearbeitung der Aufgaben kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Gruppen sein.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgende Lösung zur Konstruktion und Simulation eines einfachen Modells zu Wechselwirkungen zwischen Bruttosozialprodukt und Arbeitsplatzangebot kann Teil einer Gesamtlösung sein, bei der weitere Kleingruppe parallel arbeiten an Konstruktionen und Simulationen zu möglichen solidarischen Modellen für eine dauerhafte"Arbeit für alle!"oder auch an Analysen zur Veränderung des Arbeitsmarktes in Deutschland.
Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam auch über den Sinn und Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 bis 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 2 Schulstunden notwendig.
|
|
|
|
|
|
Konstruktion und Simulation von dynamischen Wechselwirkungen zwischen Wirtschaftswachstum und Arbeitsplätzen |
| |
|
|
| Diskutiert zunächst den Zusammenhang von Lebensqualität und Arbeit und bringt sodann das Arbeitsplatzangebot in Zusammenhang mit dem Bruttosozialprodukt. |
|
Arbeit zu haben, trägt für die meisten Menschen zur Lebensqualität bei. Denn für viele Menschen schafft Arbeit einen Sinn in ihrem Leben. Wer Arbeit hat, der fühlt sich besser!
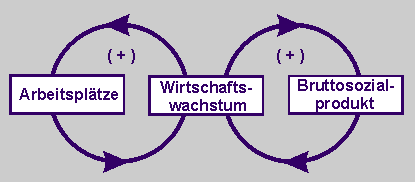
Wir nehmen an, dass sowohl die Zahl der Arbeitsplätze als auch das Bruttosozialprodukt vom Wirtschaftswachstum abhängen. Je größer das Wirtschaftswachstum ist, umso größer wird sowohl die die Zahl der Arbeitsplätze als auch das Bruttosozialprodukt. |
| |
|
|
| Beschreibt die dynamischen Wechselwirkungen zwischen Arbeitsplatzangebot und Bruttosozialprodukt in einem Wirkungsdiagramm. |
|
 |
|
|
|
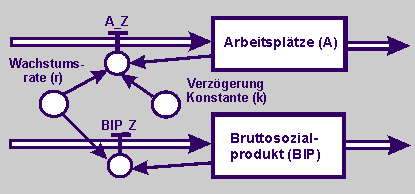
| Übertragt das Wirkungsdiagramm in ein Flussdiagramm und quantifiziert dabei auch die Größen. |
|
Auf die Zustandsgröße Arbeitsplätze (A) wirkt die Flussgröße Arbeitplatz_Zunahme (A_Z). Auf die Zustandsgröße Bruttosozialprodukt (BIP) wirkt die Flussgröße BIP_Zunahme (BIP_Z). Sowohl auf A_Z als auch auf BIP_Z wirkt einerseits dieselbe Wachstumsrate (r) als auch andererseits rückgekoppelt die bereits vorhandene Zahl an Arbeitsplätzen und das bereits erwirkte BIP. Aber das Arbeitsplatzangebot wird gegenüber dem BIP verzögert verändert (k). So wird aus dem Wirkungsdiagramm das folgende Flussdiagramm abgeleitet. |
| |
|
|
| |
|
 |
| |
|
|
| Formuliert die Dynamik in Zustandsgleichungen und weiteren Modellgleichungen. |
|
Die beiden folgenden Zustandsgleichungen für die Zustandsgrößen und die beiden Modellgleichungen für die Flussgrößen formulieren wir unter Berücksichtigung eines Zeittaktes zwischen Zustand_neu und Zustand_alt aus dem Flussdiagramm heraus.
A_neu <-- A_alt + Δt · A_Z
Anfangsgröße A = 3900 Zehn-Tausend, Δt = 0,3; Zeittakt = 1 Quartal
BIP_neu <-- BIP_alt + Δt · BIP_Z
Anfangsgröße BIP = 2900 Milliarden, Δt = 0,3; Zeittakt = 1 Quartal
A_Z = (r - k) · A Λ BIP_Z = r · BIP
r =0,025 Λ k = 0,02
Die Anfangsgrößen für Arbeitsplätze und BIP entsprechen den momentanen Zahlen in Deutschland. Wir haben sie in unterschiedlichen Maßen angegeben, damit sie im gleichen Diagramm darstellbar und vergleichbar sind. Die Konstante k haben wir experimentell bestimmt und zwar so, dass bei einer länger stabilen Wachstumsrate von etwas über 2% die Zahl der Arbeitsplätze ansteigt.
Anmerkung: Die Wachstumsrate können wir auch in den einzelnen Zeitabschnitten unterschiedlich annehmen, dann ergeben sich natürlich völlig andere Simulationsergebnisse als die folgenden.
|
|
|
|
| Programmiert das Modell in einer Excel-Tabelle auf der Grundlage der Zustands- und Modellgleichungen. |
|
Siehe hierzu:
ExcelDateien/Mappe1168a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1168a.xls (herunterladbar und interaktiv) |
| |
|
|
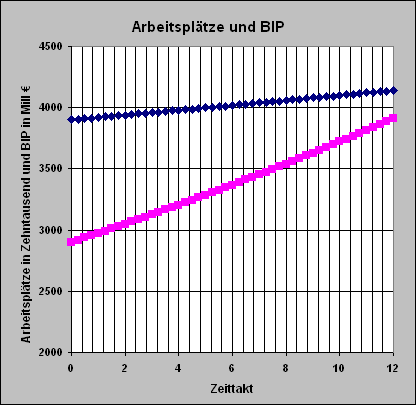
| Simuliert das Modell für unterschiedliche Anfangsgrößen und Parameter.
Anmerkung: Zur Programmierung siehe: Crash-Kurse: Einführung in die Nutzung von Excel |
|
 |
| |
|
|
| |
|
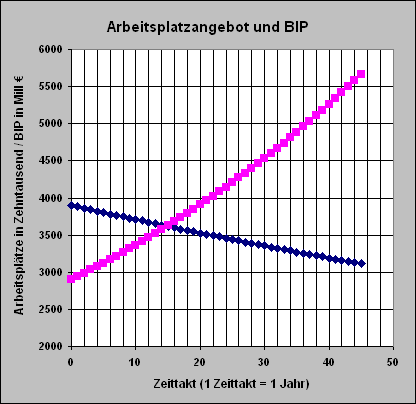
Wird Δt = 1 angenommen ( Zeittakt = 1 Jahr) und die Wachstumsrate mit
r =0,015 angenommen, so ergibt sich das folgende Bild:
ExcelDateien/Mappe1168b.htm (nur zur Ansicht) oder ExcelDateien/Mappe1168b.xls (herunterladbar und interaktiv) |
| |
|
|
| |
|
 |
|
|
|
| Beschreibt und interpretiert in Worten das Systemverhalten, den Zweck und die Grenzen des Modells. |
|
Für die Wachstumsrate nehmen wir in beiden Fällen konstant und durchgehend dieselbe Prozentzahl an. Im zweiten Fall verkleinern wir aber die Rate auf 1,5 %, also unter die Wachstumsrate von 2%, die als notwendig für das Wachsen von Arbeitsplätzen von der "Wirtschaft" angenommen wird.
Steigt das BIP, so kann es also sein, dass einerseits die Zahl der Arbeitsplätze steigt oder andererseits diese Zahl auch sinkt. Sinkt die Wachstumsrate unter 2%, so sinkt auch die Zahl der Arbeitsplätze. (Anmerkung: Dieser Zusammenhang wird auch in einer Analyse des Arbeitsmarktes untersucht.)
Je kleiner die Wachstumsrate ist, umso stärker sinkt die Zahl der Arbeitsplätze. Ist die Wachstumsrate negativ, so stürzt die Zahl der Arbeitsplätze ab. Ist die Wachstumsrate erheblich über 2%, so nimmt auch die Zahl der Arbeitsplätze erheblich zu.
Genau diese qualitativen Feststellungen können der Zweck dieses Modells sein. Somit beschreibt dieser Zweck aber auch gleichzeitig die Grenzen des Modells, die in zwei Richtungen durch weitere Modellierungen "aufgehoben" werden könnten. |
| |
|
|
| Erweitert und modelliert ggf. das dynamische Modell über die festgestellten Grenzen hinaus. |
|
Zum einen stellt sich die Frage, ob es bei dauerhaft hohem Wirtschaftswachstum überhaupt noch genügend Menschen gibt, die in Arbeit gebracht werden können. Und das ist von Land zu Land verschieden. Zum anderen ist in Zukunft wohl eher damit zu rechnen, dass die Wachstumsraten der Wirtschaft nicht mehr so üppig sind, wie sie in der Vergangenheit waren. Dann stellt sich aber die berechtigte Frage, wie sich das BIP und die Anzahl der Arbeitsplätze möglichst weitgehend entkoppeln lassen.
Im ersten Erweiterungsmodell müsste das obige Modell in einen dynamischen Zusammenhang mit dem Bevölkerungswachstum gebracht werden. Im zweiten Fall ginge es darum, „solidarische Arbeitsmodelle“ zu konstruieren, in denen auch der Begriff von Arbeit überdacht werden muss (siehe hierzu: Arbeit ist genügend vorhanden - bei neuen solidarischen Arbeitsmodellen). |
| |
|
|
| Verschriftlicht eure Ergebnisse und erstellt eine Präsentation. |
|
Wesentliche Ergebnisse sind in den ExcelMappen dargestellt. Die Interpretationen sind im vorstehenden Text zu finden. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |
















