blikk info infothek forum galerie sitemap

Quadratische, rationale sowie Wurzelfunktionen
Quadratische (und rationale) Abhängigkeiten

anfang zurueck weiter ende nach oben
  Ihr habt bei der Arbeit an realen Problemen zum Beispiel die folgenden Abhängigkeiten kennengelernt:
     
 
x
- 5,7
0
1,8
5,7
7,2
y
0
6,5
6,1
0
- 5,3
     
   
     
 
Seitenlänge (cm)
0
0,25
0,5
0,75
1
1,5
2
...
Flächeninhalt (cm²)
0
0,0625
0,25
0,5625
1
2,25
4
...
     
   
     

Quadratische Abhängigkeit:

... geschrieben als
Menge geordneter Paare

 

Die beiden voneinander abhängigen Größen bilden jeweils ein Paar. Sie sind auf folgende Weise geordnet: man nennt in dem Paar immer die vorgegebene, unabhängige Größe zuerst und dann die berechnete, abhängige Größe. Lässt man die Maßeinheiten bei den Größen fort, so kann man die Abhängigkeiten auch als Mengen von geordneten Zahlenpaaren schreiben:

Brückenbogen Ponto de Cecco:
{(-5,7/0), (0/6,5), (1,8/6,1), (5,7/0), (7,2/-5,3) ...}
Seitenlänge/Flächen-Inhalt:
{(0,0), (0,25/0,625), (0,5/0,25), (0,75/0,5625), (1,1), (1,5/2,25), (2/4) ...}

     
... geschrieben als
Paarmenge und Parabel
   Diese geordneten Zahlenpaare können als Punkte in ein geeichtes Koordinatensystem eingezeichnet werden. Auf der waagerechten Achse wird die unabhängige Größe und auf der dazu senkrechten Achse die abhängige Größe eingetragen. Zuvor müssen aber die beiden Achsen geeicht werden.
Alle Punkte der jeweiligen Paarmenge liegen auf einer Parabel. Den einzelnen (Zahlen)Paaren entsprechen jeweils die "Kreuze" auf den Parabeln. Aber zwischen diesen wenigen Kreuzen (Punkten) liegen noch viele andere Punkte auf der Parabel, die auch alle genau dieselbe Abhängigkeit beschreiben.
     
... geschrieben als Funktionsgleichung
  

Die obigen Parabeln beschreiben also viel vollständiger, als es die Wertetabellen können, die Abhängigkeiten. Diese Abhängigkeiten lassen sich sich als Paarmenge mit einer Funktionsgleichung wie folgt schreiben:

Längen-Abhängigkeit des Ponto de Cecco:

{(x/y): y = 0,2000615 x² + 6,5 }
gelesen: Menge aller Paare (x/y) für die gilt: y = 0,2000615 x² + 6,5

Seitenlänge-Inhalt-Abhängigkeit:

{(a/I): I = a · a}
gelesen: Menge aller Paare (a/I) für die gilt: I = a · a

Noch genauer betrachtet müssen für die unabhängigen Variablen
jeweils die Definitionsmengen angegeben werden. Es müssten die Mengen (oder Zahlen-Intervalle) angegeben werden, für die die Zuordnung einen Sinn ergibt.
     
Ergänzungen und Systematisierungen
  
     
 
     
Ideen für mögliche, selbstorganisierte
Übungen:
 

Der Bremsweg eines Autos lässt sich abschätzen mit: Man quadriere den 10. Teil der Geschwindigkeit, gemessen in Kilometer pro Stunde. Das Ergebnis stellt den Bremsweg in Metern dar.

  • Stelle den Term auf
  • Berechne den Bremsweg für 10km/h, 30km/m, 100km/h ...
Aufgabe: "Äpfel"
aus der PISA Studie
   Ein Bauer pflanzt Apfelbäume an, die er in einem quadratischen Muster anordnet. Um diese Bäume von dem Wind zu schützen, pflanzt er Nadelbäume um den Obstgarten herum.
Im folgenden Muster siehst du das Muster, nach dem Apfelbäume und Nadelbäume für eine beliebige Anzahl (n) von Apfelbäumen gepflanzt werden:

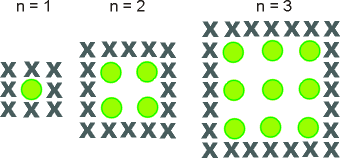
  • Vervollständige die Tabelle
n
1
2
3
4
5
Anzahl
Apfelbäume
1
4
...
...
...
Anzahl
Nadelbäume
8
...
...
...
...
  • Die Terme für die Anzahl der Apfel- und Nadelbäume lauten n² und 8n. Es gibt einen Wert für n, bei dem die Anzahlen gleich sind. Bestimme diesen Wert.
  • Angenommen, der Bauer möchte einen viel größeren Obstgarten mit vielen Reihen von Bäumen anlegen. Was wird schneller zunehmen, wenn der Bauer den Obstgarten vergrößert: die Anzahl der Apfelbäume oder die Anzahl der Nadelbäume? Erkläre, wie du zu deiner Antwort gekommen bist.

"Eine handelübliche Musik-CD"


aus "Mathematikaufgaben
für die Sekundarstufe"

 

Untersuche eine CD daraufhin, wie viel Minuten Musik auf jeden Quadratzentimeter passen. Eine Minidisc hat nur einen Durchmesser von 8cm. Wie groß ist ihre maximale Spieldauer?

Tabelliere für verschiedene CDs die Zuordnung
Breite des bespielten Rings d (in cm) --> Spielzeit t (in Minuten)
und stelle sie graphisch dar. Welchen Zusammenhang vermutest du?

  • Wie lautet die Zuordnungsvorschrift für die Zuordnung d --> t ?
  • Zeichne den Graphen und vergleiche die berechneten und die gemessenen Werte. (Woher kommen die Abweichungen?)
  • Gib zu der Zuordnung d --> t eine Umkehrfunktion t --> d an. Was leistet sie?

Auszug aus den Lösungshinweisen:

Ringbreite 3,3cm 3,5cm 2,1cm 1,2cm 2,9cm
Spieldauer 68'00'' 74'02'' 35'36'' 17'51'' 57'44
nach oben