| |
|
|
Wachstum der
Kontakt-Oberfläche
durch Verkleinern
|
|
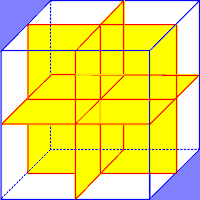
Wir nehmen an, dass der Ausgangskörper ein Würfel ist, der immer wieder in kleinere Würfel zerlegt wird.
Gegeben sei beispielsweise ein Würfel mit der Kantenlänge 10 cm. Dieser Würfel wird in kleinere Würfel aufgeteilt, die alle die Kantenlänge 5 cm haben. Die so entstehenden 8 Würfel werden dann wieder in Würfel aufgeteilt, die alle eine Kantenlänge von 2,5 cm haben. usw. usw. ...
In einer Tabelle könnt ihr für diesen Fall mögliche Wachstumsprozesse berechnen, aufschreiben und in einem Diagramm veranschaulichen:
Kantenlänge der Teilwürfel (cm) |
Anzahl der entstehenden Würfel |
Kontakt-Oberfläche aller Teilwürfel (cm²) |
10 |
1 |
600 |
5 |
8 |
1200 |
2,5 |
64 |
2400 |
... |
... |
... |
|
| |
|
|
Excell-Mappe
zur Ansicht im Browser |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappen
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
Wachstum von Oberfläche und Volumen durch Vergrößern |
|
Wir nehmen an, dass der Ausgangskörper ein Würfel ist, dessen Kantenlänge immer wieder verdoppelt wird.
Gegeben sei beispielsweise ein Würfel mit der Kantenlänge 1 cm. Wird die Kantenlänge immer wieder verdoppelt, so wachsen Oberfläche und Volumen ganz unterschiedlich.
In einer Tabelle könnt ihr für diesen Fall mögliche Wachstumsprozesse berechnen, aufschreiben und in einem Diagramm veranschaulichen:
Kantenlänge
des Würfels
(cm) |
Volumen des entstehenden Würfels
(cm³)
|
Oberfläche des entstehenden Würfels (cm²) |
1 |
1 |
6 |
2 |
8 |
24 |
4 |
64 |
96 |
... |
... |
... |
|
| |
|
|
Excell-Mappe
zur Ansicht im Browser |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm..." öffnet sich im Browser eine Excel-Mappe zu Ansicht. Sie ist nicht interaktiv. Im Internet Explorer (ältere Version) kann sie mit "Datei öffnen mit Microsoft-Excel" in eine interaktive verwandelt werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Ansichtsseite schließt. |
Interaktive Excell-Mappen
im Browser öffnen |
|
|
| |
|
Mit Klick auf "Excel-Tabelle und -Diagramm ... " öffnet sich im Browser ein Fenster zum Dateidownload. Mit "öffen" aktivieren und OK wird die Excel-Mappe geöffnet und ist interaktiv. Sie kann auch auf den eigenen Rechner geladen werden.
Zu dieser Seite kommt ihr zurück, indem ihr die Excel-Mappe schließt. |
| |
|
|
|
|
|
| |
|
|
| Ideen für mögliche, selbstorganisierte
Übungen:
| |
Experimentiert mit der obigen Exel-Mappe zum "Wachsen" der Kontakt-Oberfläche durch "Verkleinern":
- Wie groß wird die gesamte Kontak-Oberfläche nach 5maligem, 10maligen ... Teilen, wenn
der Ausgangswürfel unterschiedliche Kantenlängen (100 cm, 50cm, 25cm, ...) hat.
- Veranschaulicht jeweils in einem Diagramm die unterschiedlichen Abhängigkeiten.
- Findet die Terme für die jeweiligen Zuordnungen und schreibt die entsprechende Funktionsgleichung auf.
- Erstellt selbst eine Excel-Mappe für unterschiedliche Teilungsprozesse (halbieren, dritteln, vierteilen, ...).
- Wann wird die Kontakt-Oberfläche sehr schnell, sehr groß?
- Recherchiert für diesen Sachverhalt auch Anwendungsfälle aus der Nanotechnik?
- Erstellt selbst eine Excel-Mappe für andere Körper als Würfel.
Experimentiert ebenfalls mit der obigen Exel-Mappe zum "Wachsen" von Oberfläche und Volumen durch "Vergrößern".
- Findet die Terme für die Zuordnungen und schreibt die entsprechende Funktionsgleichung auf.
- Erstellt selbst eine Excel-Mappe für andere Körper als Würfel.
|
| |
|
|
Ergänzungen und Systematisierungen |
|
|