blikk info infothek forum galerie sitemap

Quadratische, rationale sowie Wurzelfunktionen
Quadratische Funktion - Systematisierungen

anfang zurueck weiter ende nach oben

  Ihr habt bei der Arbeit an realen Problemen die beiden folgenden quadratischen Abhängigkeiten kennengelernt.
     
 
Die Abhängigkeit des Ponto de Cecco
{(x/y) / y = 0,2000615 · x² + 6,5}
     
 
     
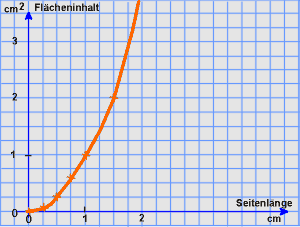
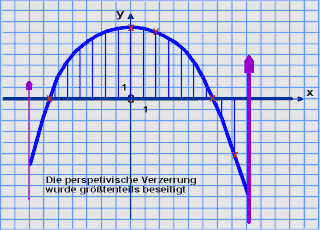
Worin unterscheiden sich die beiden Parabeln voneinander?
   Die linke Parabel ist ein Beispiel für ein halbe Normalparabel. Denn bei einem Quadrat gibt es keine negativen Seitenlängen.
Die linke Parabel ist zwar vollständig, aber sie ist nach unten geöffnet und schneidet die y-Achse bei 6,5.
   
Die Normalparabel
  

Stellt man aber in einem x/y-Koordinatensystem die abstrakte Funktionsgleichung

y = x² oder f(x) = x²

dar, so erhält man als Graph die Normalparabel.

     
Scheitelpunkt der Parabel
   Den tiefsten oder höchsten Punkt einer Parabel nennt man ihren Scheitel.
Die Normalparabel hat ihren Scheitelpunkt bei (0/0).
Die Parabel des Ponto de Cecco hat ihren Scheitelpunkt bei (0/6,5).
Lässt sich aus einer quadratischen Funktionsgleichung der Scheitel der Parabel ablesen, so spricht man von einer Scheitelpunktsform.
     

Experimente mit
Scheitelpunktsformen

 

  

Auf der Seite

findet ihr Aufgaben, um mit den folgenden abstrakten, quadratischen Funktions-Formen zu experimentieren.

f(x) = a · x² ...... ..oder....... y = a · x²
f(x) = (x+d)² ........oder....... y = (x+d)²
f(x) = (x + d)² + e ......ooder....... y = (x + d)² + e

Diese Formen gestatten es, den Scheitel der Parabeln abzulesen.
     
Normalform der Parabel
  

Die Scheitelpunktsform ist eine besonders ausgezeichnete Form, die auch in der Regel in Anwendungssituationen vorkommt. Noch einmal abstrakter ist aber die Normalform der quadratischen Funktions-Form:

f(x) = ax² + bx +c ....oder.......y = ax² + bx +c

An dieser Form lässt sich der Scheitel der Parabel nicht mehr ablesen.

Setzt man aber in dieser Form y = 0, so erhält man eine quadratische Gleichung mit der Variablen x. Die Lösungen dieser Gleichung bestimmen die Schnittpunkte mit der x-Achse.
Setzt man in dieser Form x = 0, so erhält man eine Gleichung mit der Variablen y. Die Lösung dieser Gleichung bestimmt den Schnittpunkt mit der y-Achse.
     
 
     

Ideen für mögliche, selbstorganisierte
Übungen:

Freier Fall,
Anhalteweg und mehr ...

  
  • Die Gleichung s = 1/2 g · t² (mit der Erdbeschleunigung g = 9,814m/s²) beschreibt die Fallstrecke in Abhängigkeit von der Zeit. Ein Stein fällt in einen Brunnen. Den Aufprall hört man nach 2,8 s.
    Wie tief ist der Brunnen? Die Schallgeschwindigkeit beträgt 340m/s.
  • Die Gleichung s = v²/2a + vt, mit a als Verzögerung und t als Reaktionszeit, beschreibt den Anhalteweg eines Fahrzeugs.
    Ein Pkw verzögert mit a = 9 m/s².
    a) Wie lang ist der Anhalteweg bei einer Geschwindigkeit von 80km/h und einer Reaktionszeit von 0,5 s?
    b) 20 m vor dem Pkw springt ein Kind auf die Straße. Wie groß darf die Geschwindigkeit bei einer Reaktionszeit von 0,5 s höchstens sein, damit das Kind nicht überfahren wird?

Verweise auf Angebote außerhalb dieser Lernumgebung
 

Das online-Lexikon wikipedia bietet vertiefende Informationen
   

Experimentiert auch mit den Schiebereglern und Animationen zu Parabelwelten und Hyperbeln auf den interaktiven Seiten des Mathematischen Instituts der Uni Wuppertal.

nach oben