Exponential-, Logarithmus- und logistische Funktionen
Bestimmen von Exponentialfunktionen

Im Kapitel "ein linearer oder ein exponentieller Prozess?" findet ihr verschiedene Möglichkeiten, wie man graphisch oder mit Hilfe von Werkzeugen Funktionen findet, die eine gegebene Datenwolke gut modelliert.

algebraische Möglichkeiten

Hier geht es nun um die Möglichkeit, eine Exponentialfunktion, die einen exponentiellen Prozess beschreibt, auch selbst rechnerisch zu ermitteln.

Als erstes solltet ihr die Quotienten zwischen euren Funktionswerten in gleichen zeitlichen Abständen berechnen. Wenn sie etwa gleich sind, liegt ein exponentieller Prozess vor und ihr müsst nur noch einen Anfangswert festlegen und den Wachstumsfaktor berechnen.

Als Anfangswert könnt ihr den Wert zur Zeit t = 0 verwenden. Für den Wachstumfaktor ist der Durchschnitt der Quotienten geeignet. Hier dürft ihr aber nicht das bekannte arithmetische Mittel verwenden. Für den Mittelwert von Faktoren verwendet man das geometrische Mittel

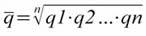
wobei q1, q2, ... qn die einzelnen Quotienten darstellen.

Ein einfaches Beispiel, wie ihr das in Excel realisieren könnt, könnt ihr euch im Folgenden herunterladen. Bedenkt, dass ihr in Excel die n-te Wurzel durch "hoch 1/n" berechnen könnt.

Beispiel: Windenergiekapazitäten weltweit

Ebenso könnt ihr auch entsprechende Funktionen bestimmen, wenn ihr bestimmte Informationen über einen exponentiellen Prozess habt bzw. vorgebt. Beispiele:

1. Ein Kapital von 1000 Euro wird monatlich mit 3% verzinzt.

Also beträgt der Wachstumsfaktor q = 1 + r = 1,03

2. Die Erdölproduktion stieg von 3486 Mio. t im Jahr 1997 auf 3996 Mio. t in 2011.

Für 14 Jahren beträgt der Faktor 3996/3486. Den Steigerungsfaktor pro Jahr erhält man als 14. Wurzel daraus.

3. Die Halbwertzeit von Caesium-137 beträgt 30 Jahre.

Der Zerfallsfaktor für 30 Jahre beträgt 0,5. Also ist der gesuchte Zerfallsfaktor für ein Jahr die 30. Wurzel daraus. Als Startwert könnt ihr ihr 100% (bzw. 1) verwenden.

Im Zusammenhang mit dem realen Problem "Wohlstand für alle" können Tilgungspläne helfen, die Problematik besser zu verstehen. Unter "Fallbeispiel für einen Tilgungsplan" ist dies auch ausgeführt.

• Sucht mit Hilfe von Excel oder Geogebra die Funktionsgleichung für die Zinsen oder die Restschuld. Das kann experimentell und algebraisch erfolgen.
• Macht euch klar, wie groß jeweils die Wachstumsrate bzw. der -faktor ist.