Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen (9) 10 bis 12 |
| |
|
|
| Hinweis:
Die Bearbeitung der Aufgaben zu "Konstruktionen und Simulationen zur Dynamik der Welternährung" kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Gruppen sein.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgende Lösung zu Konstruktionen und Simulationen zur Dynamik der Welternährung kann Teil einer Gesamtlösung sein, bei der weitere Kleingruppen parallel arbeiten an dynamischen Modellen zum Wachsen einer Bevölkerung oder auch an Modell-Experimenten zum Wachsen von Bevölkerungen unter der Annahme von unterschiedlichen Bedingungen oder auch an einer Analse zum Wachstum einer Bevölkerung.
Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam auch über den Sinn und Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 bis 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 2 Schulstunden notwendig. |
| |
|
|
|
|
|
|
|
Konstruktionen und Simulationen zur Dynamik der Welternährung |
| |
|
|
| Diskutiert in eurer Kleingruppe das Problem: Wie viel Menschen kann die Erde überhaupt ernähren? |
|
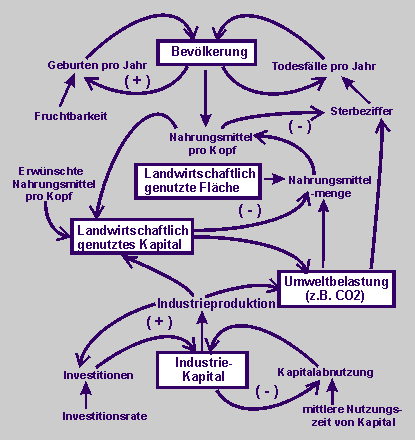
Wir fragen uns, wovon eine hinreichende Welternährung abhängt. Dazu nutzen wir zunächst das folgende komplexe Wirkungsdiagramm, das die Teilstruktur "Landwirtschaft und Kapital" im komplexen Wirkungsgefüge von "Bevölkerung, Kapital, Landwirtschaft und Umweltverschmutzung" aus dem Bericht an den Club of Rome "Die Grenzen des Wachstums" zeigt (S 83). |
| |
|
|
|
|
 |
| |
|
|
| Entscheidet euch und begründet, welche Größen ihr miteinander in Beziehung bringen wollt.
|
|
Dieses Wirkungsgefüge ist sehr komplex. Daher entscheiden wir uns, zunächst den folgenden Ausschnitt daraus zu untersuchen. Außerdem nutzen wir dabei auch die folgenden Sachinformationen aus dem Bericht "Die Grenzen des Wachstums".
Wenn die Nahrungsmittelmenge pro Kopf unter das von der Bevölkerung verlangte Maß fällt, entsteht eine Tendenz, das landwirtschaftliche Kapital zu erhöhen, so dass die Nahrungsmittelerzeugung wieder gesteigert werden kann und zu einer Erhöhung der Nahrungsmittelmenge pro Kopf führt." (S 85).
|
|
|
|
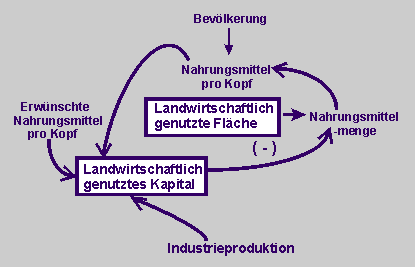
| Erstellt für die ausgewählten Größen ein Wirkungsdiagramm.
(Ausschnitt aus dem obigen komplexen Diagramm) |
|
 |
|
|
|
| Bestimmt nun die Zustands- und Flussgrößen sowie die Parameter, die ihr in diesem dynamischen Modell untersuchen wollt. |
|
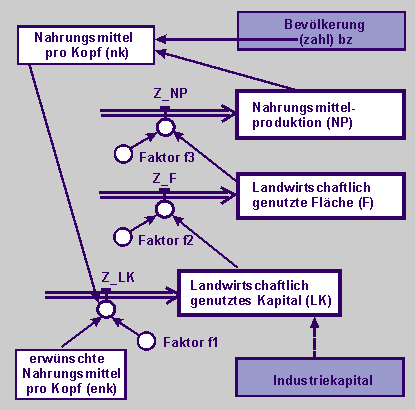
Die Bevölkerungszahl (bz) nehmen wir in unserem Modell zunächst als eine konstante Größe an. Das Kapital für die Industrieproduktion übernehmen wir als Anfangsgröße in die Zustandsgröße "Landwirtschaftlich genutztes Kapital (LK)". Weitere Zustandsgrößen (oder Bestandsgrößen), die wir untersuchen wollen, sind die "Landwirtschaftlich genutzte Fläche (F)" und die "Nahrungsmittelmenge bzw. die "Nahrungsmittelproduktion (NP)".
Diese Bestandsgrößen haben jeweils einen Zuwachs: Mit dem eingesetzten Kapital wächst die nutzbare Fläche und mit der nutzbaren Fläche wächst die produzierte Nahrungsmenge. Entsprechend gibt es also die drei folgenden Flussgrößen Zunahme_landwirtschaftliches Kapital (Z_LK), Zunahme_landwirtschaftlich genutzte Fläche (Z_F) und Zunahme_Nahrungsmittelproduktion (Z_NP), auf die jeweils ein Anpassungsfaktor f1, f2 und f3 wirkt.
Die wirkliche Nahrungsmenge pro Kopf (nk) und die erwünschte Nahrungsmenge pro Kopf (enk) erzeugen einen Rückkopplungskreis über das eingesetzte Kapital.
Auf der Grundlage dieser Überlegungen entsteht dann das folgende, mögliche Flussdiagramm. |
| |
|
|
| Stellt sodann dieses Modell in einem Flussdiagramm dar. |
|
 |
| |
|
|
| |
|
"Wichtigste Grundlage für die Nahrungsmittelproduktion ist bebaubares Land. Nach neueren Untersuchungsergebnissen gibt es auf der Erde etwa 3,2 Milliarden Hektar prinzipiell landwirtschaftlich nutzbare Flächen. Die Hälfte davon, und zwar die ertragreichere, leicht bebaubare Hälfte, wird bereits landwirtschaftlich genutzt. Für die andere Hälfte sind hohe Kapitalsummen für Bewässerung, Rodung, Düngung und ähnliche Maßnahmen der Urbarmachung erforderlich, wenn man sie ebenfalls nutzen will. Die Durchschnittskosten in unbesiedelten Gebieten belaufen sich auf etwa 1150 Dollar pro Hektar (ha)" .... (S. 39) ...
"Jeder Mensch benötigt bei der gegenwärtigen Produktionsrate etwa 0,4 ha zu seiner Ernährung." (S. 40).
Auf der Grundlage dieser Feststellungen des Club of Rome lassen sich die Anfangsgrößen für LK, F, und NP berechnen und auch die Faktoren f1, f2 und f3 experimentell bestimmen bzw. abschätzen.
Der Wert für enk lässt sich wie folgt berechnen: enk = 0,26 Tonnen Weizen pro Jahr pro Kopf entsprechen 0,72 kg pro Kopf pro Tag. Diese Menge entspricht dem Normalverbrauch von rund 3000 kcal pro Kopf pro Tag, bei 1g Kohlenhydrate = 4,2 kcal.
(Die wirkliche Nahrungsmenge nk ist die gelbe Linie in den folgenden Simulationen).
|
|
|
|
| Formuliert die Dynamik in Zustands- und Modellgleichungen und belegt die Größen mit Werten.
|
|
Aus diesem Flussdiagramm abstrahieren wir sodann die folgenden Zustands- und Modellgleichungen und belegen die Anfangsgrößen und die Konstante sowie die Faktoren mit Werten. Die Werte lassen sich aus den obigen Sachinformationen oder aus den Sachinformationen zum realen Problem "Bevölkerungsexplosion" abschätzen.
LK_neu <-- LK_alt + Δt · Z_LK
Anfangsgröße LK = 0,08 Billionen €;
Δt = 0,005;
F_neu <-- F_alt + Δt · Z_F
Anfangsgröße F = 1,5 Mill. ha;
NP_neu <-- NP_alt + Δt · Z_NP
Anfangsgröße NP = 1,5 Bill. Tonnen;
Z_LK = (enk - nk) · f1 Λ F = LK · f2 Λ
Z_NP = F · f3 Λ nk = NP/ bz
enk =0,26 Tonnen Weizen pro Jahr pro Kopf
Λ f1 = 25 Λ f2 = 25 Λ f3 = 2 Λ bz = 6,8 Milliarden
|
|
|
|
| Programmiert das Modell mit Excel. |
|
Siehe hierzu:
ExcelDateien/Mappe1229c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1229c.xls (herunterladbar und interaktiv) |
| |
|
|
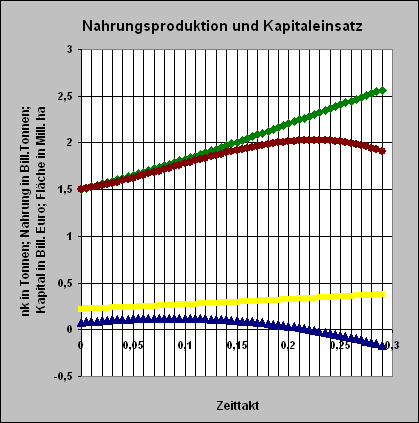
Simulationsergebnisse; die Zeitachse ist im Zeittakt geeicht!
Grün: Nahrung
Braun: Fläche
Blau: Kapital
Gelb:
Nahrungsmenge
pro Kopf
pro Jahr in Tonnen |
|
 |
| |
|
|
| Anmerkungen zur Interpretation des Zeittaktes |
|
Die Randbedingungen des Systems – oben fett gedruckt – belegen und begrenzen das mathematische Gleichungssystem mit relativ festen Größen. Sollen sie in der schrittweise berechneten Lösung des Gleichungssystems repräsentiert werden sowie interpretierbar sein, so wird bei den gegebenen Randbedingungen innerhalb gewisser Grenzen ein Δt = 0,005 simulativ-experimentell als sinnvoll erzwungen. Doch die Zeitachse im Zeittakt der schrittweise berechneten Lösung bliebe dabei immer noch frei von einer Maßeinheit. Nachträglich erlauben die obigen Randbedingungen eine Interpretation des Zeittaktes als 1 Jahr.
Natürlich ist diese Interpretation – auch unter den gegebenen Randbedingungen - nicht die einzig mögliche. Bei Änderung der Faktoren f1, f2 und f3 (also von speziellen dimensionslosen Randbedingungen) sind auch andere Werte für Δt simulativ experimentell zu finden. Immer bleibt es aber wichtig, dass die Zeitachse so zu interpretieren ist, dass die wichtigen Randbedingungen im Diagramm wiedererkennbar sind.
Siehe hierzu auch die Ausführungen auf Seite 7460.htm. |
| |
|
|
Dasselbe Simulationsergebnis wie zuvor aber der Zeittakt wurde mit 1 Jahr interpretiert
Grün: Nahrung
Braun: Fläche
Blau: Kapital
Gelb:
Nahrungsmenge
pro Kopf
pro Jahr in Tonnen
|
|
|
| |
|
|
| |
|
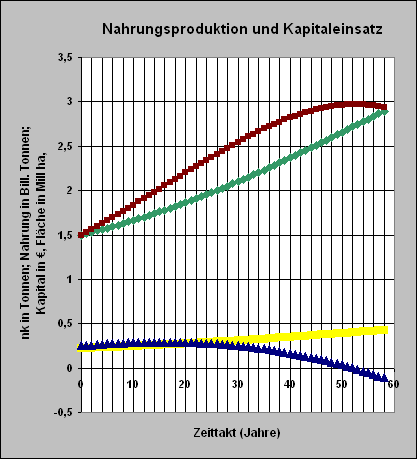
Halten wir alle Werte bei, erhöhen aber den Kapitaleinsatz auf Lk = 0,25 Billionen Euro, dann ergibt sich das folgende Simulationsergebnis.
Siehe hierzu:
ExcelDateien/Mappe1229d.htm (nur zur Ansicht) oder ExcelDateien/Mappe1229d.xls (herunterladbar und interaktiv) |
| |
|
|
| |
|
 |
| |
|
|
| |
|
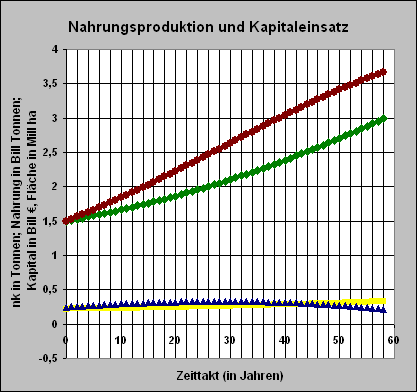
In einer dritten Simulation nehmen wir an, dass sich die Bevölkerungszahl stetig erhöht. Dabei gehen wir von einer mittleren Variante in der Prognose aus: In 40 Jahren erhöht sich die Bevölkerungszahl von 6,8 Milliarden auf 8,6 Milliarden. Das entspricht einem linearen Anstieg von 0,04. Diesen Anstieg programmieren wir in die Spalte bz ein und erhalten dann das folgende Simulationsergebnis:
Siehe hierzu:
ExcelDateien/Mappe1229e.htm (nur zur Ansicht) oder ExcelDateien/Mappe1229e.xls (herunterladbar und interaktiv) |
| |
|
|
| |
|
 |
|
|
|
| Beschreibt und interpretiert in Worten das Systemverhalten, den Zweck und die Grenzen des Modells. |
|
Mit zunehmend mehr eingesetztem Kapital (siehe zweite Simulation) nimmt die landwirtschaftlich nutzbare Fläche und ebenso die Nahrungsproduktion zu.
Nähert sich die wirklich nutzbare Nahrungsmenge (pro Kopf) der gewünschten Nahrungsmenge (pro Kopf) an, so nimmt der Kapitaleinsatz ab und zeitverzögert auch die bewirtschaftete Fläche.
Aus der zweiten Simulation ergibt sich weiter, dass bei einem Kapitaleinsatz von LK = 0,25 Billionen Euro in etwa 30 Jahren bereits alle Menschen genügend Nahrung hätten. Ab da sinkt dann der notwendige Kapitaleinsatz, und auch die urbar gemachte Fläche nimmt weniger schnell zu, nähert sich einem Maximum und fällt dann ab.
Bei steigender Bevölkerung wird erst sehr viel später erreicht, dass alle Menschen genügend Nahrung haben.
Die Fläche, die urbar gemacht werden kann, wird erreicht. Der Kapitaleinsatz bleibt nahezu erhalten und die Nahrungsproduktion bleibt zwar dieselbe. Alles muss aber auf sehr viel mehr Menschen aufgeteilt werden.
Genau diese mehr qualitativen Feststellungen könnten der Zweck dieses Modells sein. Der Zweck ist also eine Formulierung von möglichen Visionen und kein Vorhersagemodell, es sei denn, es wird wahrgenommen, dass das Problem einer hinreichenden Ernährung aller Menschen nicht alleine über die urbar gemachte Fläche gelöst werden kann. Dieser Zweck beschreibt gleichzeitig auch die Grenzen des Modells. Zu fragen ist, ob mittels Gentechnik, die heute noch auf rigorose Ablehnung stößt, die Nahrungsmenge erneut erhöht werden kann. Siehe: Gen- und biotechnische Evolution: Mehr Chancen als Risiken?
|
| |
|
|
| Verschriftlicht eure Ergebnisse und erstellt eine Präsentation. |
|
Wesentliche Ergebnisse sind in den ExcelMappen dargestellt. Die Interpretationen sind im vorstehenden Text zu finden. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |