Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung;
bezogen auf die Klassen (9) 10 bis 12 |
| |
|
|
| Hinweise:
Die Bearbeitung der folgenden Aufgaben kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Kleingruppen.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgenden Lösungen zur
können Teil einer Gesamtlösung sein, bei der weitere Kleingruppen parallel arbeiten an Konstuktionen und Simulationen zu unterschiedlichen Szenarien auf dem Hintergrund energie- und klimapolitischer Diskussionen.
Nach der Präsentation und Diskussion der Gruppenlösungen in der Klasse wird gemeinsam u.a. über den Sinn und Zweck dynamischer Modellierungen diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 bis 5 Schulstunden notwendig, wenn auch Teilaufgaben zu Hause erledigt werden. Der Einsatz eines Werkzeugs z.B. Excel ist notwendig. Für eine Diskussion in der Klasse sind dann noch einmal 2 Schulstunden notwendig. |
| |
|
|
|
|
|
|
|
Konstruktion und Simulation
eines Grundmodells von Wechselwirkungen
zwischen Bevölkerung, Energie und Kohlendioxid |
| |
|
|
| Konstruiert und Simuliert Wechselwirkungen zwischen Bevölkerungswachstum, Umwandlung von fossiler Energie und Ausstoß von Kohlendioxid auf der Erde.
|
|
Wir beschränken uns zunächst auf ein sehr einfaches Grund-Modell, das mögliche Wirkungen (Abhängigkeiten oder Bindungen) zwischen der Erd-Bevölkerung, dem Bedarf und der Umwandlung von alleine fossilen Energieträgern und dem darauf basierenden Ausstoß an Kohlendioxid beschreibt.
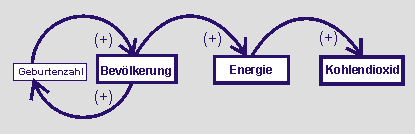
Das Wirkungsdiagramm zeigt erstens, wie die Geburtenzahl positiv auf das Wachsen der Erd-Bevölkerung wirkt und die wachsende Bevölkerung positiv auf die Geburtenzahl zurückwirkt. Je mehr Menschen leben, desto mehr Kinder werden geboren.
Zweitens zeigt das Wirkungsdiagramm, dass die zunehmende Bevölkerung positiv auf den Bedarf an Energie und die Umwandlung von Energie wirkt. Wobei angenommen wird, dass es sich bei den Energien nur um fossile handelt. Je mehr Menschen die Erde bewohnen, desto mehr Energie wird benötigt und umgewandelt.
Drittens zeigt das Wirkungsdiagramm, dass je mehr fossile Energien umgewandelt werden desto mehr CO2 in die Atmosphäre gelangen wird.
Das Wirkungsdiagramm beschreibt die Abhängigkeiten in qualitativer Form. Es wird gefragt, Was wirkt auf Was und wie. Argumentiert wird mit dem Pluszeichen oder mit „je desto“. |
| |
|
|
| Zeichnet dazu zunächst ein Wirkungsdiagramm. |
|
 |
| |
|
|
Diskutiert sodann in eurer Kleingruppe mögliche Zustandsgrößen, Flussgrößen, Parameter und Konstante in diesem Modell.
Zum Begriff "Wachstumsziffer" siehe "Wachstumszahlen, -Ziffern und -Raten sowie u.a. Arbeitslosen-Quoten" |
|
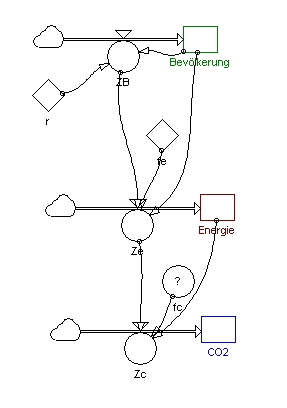
Wir übertragen das Wirkungsdiagramm in ein Flussdiagramm indem wir überlegen, welche Zustandsgrößen, Flussgrößen und Raten wir abstrahieren können.
Die Zustandsgrößen sind leicht erkennbar: Bevölkerungszahl (B), Gesamtmasse der umgewandelten fossilen Energie (E) und Gesamtmasse des ausgestoßenen Kohlendioxids (C).
Die Flussgrößen müssen im Einzelnen überlegt werden. Auf die „Bevölkerungszahl“ wirkt die Flussgröße „Zunahme_Bevölkerung“ (Zb) mit einer Wachstumsziffer pro Mensch pro Jahr (r), die aber von der bereits vorhandenen Erd-Bevölkerungzahl abhängt.
Zur "Gesamtmasse der bereits umgewandelten fossilen Energie“ kommt jeweils die „Zunahme_Energie“ (Ze) hinzu. Sie hängt zu einen mit einem Faktor (fe=„Modernisierungsfaktor“) von der Bevölkerungszahl ab, zum anderen von Zb mit einem Umwandlungsfaktor von rund 2,5 Mio. Wh pro Mensch und Jahr.
Zur „Gesamtmasse des bereits ausgestoßenen Kohlendioxids“ kommt jeweils die Flussgröße „Zunahme_Kohlendioxid“ (Zc) hinzu. Sie hängt zum einen mit einem Faktor (fc = Ausnutzungsfaktor) von der jeweiligen Gesamtmasse der umgewandelten fossilen Energie ab, zum anderen von Ze und einem Umwandlungsfaktor von 1,85 t CO2 pro MWh. Der Gehalt an Kohlendioxid in der Atmosphäre wird mit einer Massengröße beschrieben.
|
|
|
|
| Stellt das Modell in Form eines Flussdiagramms dar.
Akürzungen:
B = Bevölkerung
Zb = Zunahme_Bevölkerung
r = Wachstumsziffer pro Mensch pro Jahr (auch Wachstumsrate genannt)
E = fossile Energieumwandlung
Ze = Zunahme_Energie
fe = Moderinsierungsfaktor
C = Kohlendioxid
Zc = Zunahme_Kohlendioxid
fc = Ausnutzungsfaktor |
|
|
|
|
|
| Beschreibt die Wechselwirkungen (bzw. die direkten Abhängigkeiten) in Zustands- und Modellgleichungen. |
|
In den folgenden Zustands- und Modellgleichungen, die sich aus dem Flussdiagramm unter Berücksichtigung eines Zeittaktes zwischen Zustand_alt und Zustand_neu erschließen lassen, wird das Modell noch einen weiteren Schritt quantifiziert, indem alle Größen mit Zahlen belegt werden. B_neu <-- B_alt + Δt · Zb;
Anfangsgröße B = 6,8 Milliarden; Δt = 1 (Zeittakt 1 Jahr)
E_neu <-- E_alt + Δt · Ze;
Anfangsgröße E = 16,8 Mio. GWh; Δt = 1 (Zeittakt 1 Jahr)
C_neu <-- C_alt + Δt · Zc;
Anfangsgröße C = 31 Milliarden Tonnen; Δt = 1 (Zeittakt 1 Jahr)
Zb = r · B; r = 0,013 (daher Zeittakt 1 Jahr)
Ze = fe · B +
Zb*2,5
; fe = 0,01
Zc = fc · E
+ Ze*1,85
; fc = - 0,005
Zur Bestimmung der Anfangsgrößen und der Wachstumsziffer der Erdbevölkerung sowie zur Abschätzung der Binde-Faktoren wird auf die folgenden Sachinformationen verwiesen (Wachstum der Weltbevölkerung, Energie-"Verbrauch" , Energiegewinnung aus fossilen Energieträgern sowie Ausstoß von Kohlendioxid). Die Anfangsgrößen beziehen sich etwa auf das Jahr 2008. Aber die beiden Binde-Faktoren fe und fc hängen auch vom Zweck des Modells ab.
Mindestens müssen diese beiden Faktoren aber so robust sein (siehe ma1919.htm), dass das Modell mathematisch interpretierbar ist und in einem Intervall auch bleibt. Dieses Intervall brauchen wir für eine Interpretation in die Wirklichkeit.
Die beiden Umwandlungsfaktoren ergeben sich als Quotienten der bekannten Zahlen E/B und C/E. |
| |
|
|
Programmiert die Zustands- und Modellgleichungen und simuliert das konstruierte Modell.
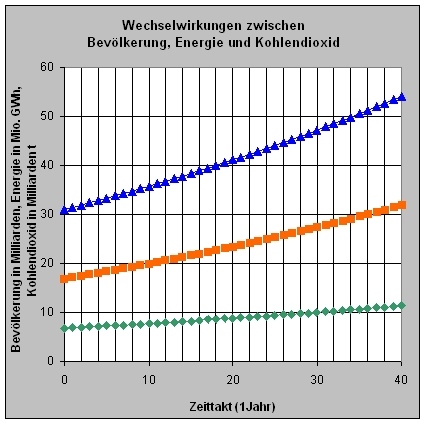
blau = Kohlendioxid;
rot = Energie;
grün = Bevölkerung
|
|
Die programmierte - und damit simulierbare - Tabelle und auch ein Simulationsergebnis siehe:
ExcelDateien/Mappe1558na.htm (nur zur Ansicht) oder ExcelDateien/Mappe1558na.xls (herunterladbar und interaktiv)
Hier ein mögliches Simulationsergebnis, das zur Tabelle passt:
|
| |
|
|
| |
|
In der Excel-Tabelle lassen sich aber alle stärker unterlegten Werte ändern. Geschieht dies z.B. durch Anheben der Wachstumsziffer auf
r = 0,02 und der Faktoren
für den Modernisierungs- und Suffizienzeffekt auf
fe = 0,02 und fc = -0,01 , so ergibt das folgende Simulationsergebnis.
Siehe hierzu:
ExcelDateien/Mappe1558nb.htm (nur zur Ansicht)
ExcelDateien/Mappe1558nb.xls (herunterladbar und interaktiv)
Viele weitere Simulationen sind möglich. Eine Veränderung der Anfangsgrößen führt in der Regel nur zu einer Verschiebung der Punkt-Diagramme auf der Hoch-Achse (y-Achse). |
|
|
|
| Beschreibt das Verhalten dieses einfachen Modells, interpretiert es und beschreibt den Zweck und die Grenzen dieses Modells. |
|
In diesem einfachen Grundmodell wächst mit der Bevölkerungszahl auch die Nachfrage nach Energie. Sie besteht – so wird hier angenommen - ausschließlich aus fossilen Energieträgern, weil diese z.B. in den bevölkerungsreichsten Ländern der Erde (wie China) reichlich vorhanden sind und daher zur Energieumwandlung genutzt werden. Entsprechend steigt der Ausstoß an Kohlendioxid. Die drei Zustandsgrößen hängen direkt von einander ab. Ihre Entwicklungen verlaufen gleichförmig.
Die Modellierung endet also - nach einer quantitativen Phase - mit einer Verhaltensbeschreibung, die wieder qualitativer Natur ist. Sie vermittelt grundlegende (qualitative) Einsichten. Sie führt aber auch zu einer neuen, weiterführenden Frage: Was würde z.B. geschehen, wenn die Klima-Weltkonferenzen einen Erfolg gehabt hätten und in Zukunft immer mehr Energie wirklich aus erneuerbaren Quellen stammen würde? Darauf gibt das einfache Grundmodell keine Antwort mehr. Eine Modellerweiterung wird notwendig. |
|
|
|
|
|
Konstruktion und Simulation von Wechselwirkungen
zwischen Bevölkerung, Energieumsatz und Kohlendioxid
unter der Annahme eines Energiemixes aus fossilen und erneuerbaren Energien |
| |
|
|
| Konstruiert und simuliert in einem Modell dynamische Wechselwirkungen zwischen Bevölkerungswachstum, fossiler Energieumwandlung und Ausstoß von Kohlendioxid auf der Erde, unter der Annahme, dass immer mehr fossile Energie durch erneuerbare ersetzt wird. |
|
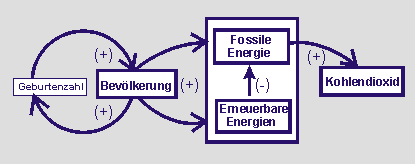
Das obige Wirkungsdiagramm und alle obigen qualitativen Beschreibungen bleiben im Prinzip erhalten.
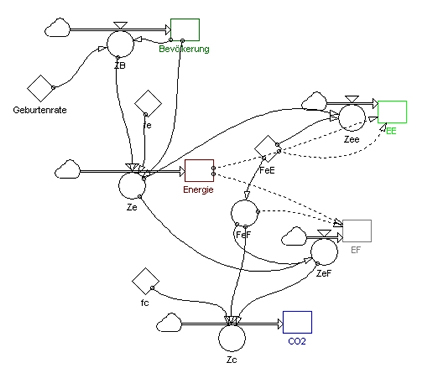
Ergänzend wird nun angenommen, dass sich die von der Bevölkerung geforderten Energien (E) aufteilen in einen Energiemix, der lediglich zwischen fossilen Energien (FE) und erneuerbaren Energien (EE) unterscheidet. Nur die fossilen Energien haben, wie hier angenommen wird, eine Erhöhung des Kohlendioxids in der Atmosphäre zur Folge. Je mehr erneuerbare Energien aber verfügbar sind oder sein werden, desto weniger fossile müssen umgewandelt werden.
Das folgende Wirkungsdiagramm beschreibt diese Abhängigkeiten in qualitativer Form. Es wird mit dem Minuszeichen oder mit „je desto“ argumentiert. |
| |
|
|
| Zeichnet ein Wirkungsdiagramm. |
|
 |
| |
|
|
| Diskutiert sodann in eurer Kleingruppe mögliche Zustandsgrößen, Flussgrößen, Parameter und Konstante in diesem Modell. |
|
Für die Aufteilung der gesamten, von der Bevölkerung gewollten Energie (E) wird ein Mix aus fossilen Energien (FE) und erneuerbaren Energien (EE) angenommen.
Im Fall A wirken zwei Faktoren feE und ein Faktor feF. Aber die Summe dieser beiden Faktoren ist 1, damit im Modell die Gesamt"menge" an Energie nur aufgeteilt wird.
Im Fall B werden die beiden Faktoren als zeitabhängige Funktionen mit feE(t) + feF(t) = 1 beschrieben. So kann modelliert werden, dass die "öffentliche Meinung" eine Zunahme der Erneuerbaren Energien will.
Aber nur der Anteil EF wirkt mit einem Faktor fc auf eine Steigerung des Kohlendioxids C in der Atmosphäre. Er wird, wie bereits im vorhergehenden Modell, mit einer Massengröße beschrieben. |
| |
|
|
| Zeichnet ein Flussdiagramm und beschreibt die Wechselwirkungen in Zustands- und Modellgleichungen. |
|
 |
| |
|
|
| Beschreibt die Wechselwirkungen in Zustands- und Modellgleichungen.
|
|
Die folgenden Zustands- und Modellgleichungen lassen sich unter Berücksichtigung eines Zeittaktes zwischen Zustand_alt und Zustand_neu aus dem Flussdiagramm erschließen. Das Modell wird also noch einen weiteren Schritt quantifiziert, indem wieder alle Größen mit Zahlen oder auch Funktionen belegt werden.
B_neu <-- B_alt + Δt · Zb;
Anfangsgröße B = 6,8 Milliarden; Δt = 1 (Zeittakt 1 Jahr)
E_neu <-- E_alt + Δt · Ze;
Anfangsgröße E = 16,8 GWh; Δt = 1 (Zeittakt 1 Jahr)
C_neu <-- C_alt + Δt · Zc;
Anfangsgröße C =31 Mill. Tonnen; Δt = 1 (1 Jahr)
Zb = r · B; r = 0,013
Ze= fe · B + Zb*2,5; fe = 0,01
Zc= fc · FE + Ze*2,12; fc = - 0,005
EE = feE · E · (1-fc); feE = 0,13;
FE = feF · E · (1-fc); feF = 1 - feE
Fall B:
EE = feE(t) · E · (1-fc); feE(t) = feE(t-1)*(1+p); p = 0,05
FE = feF(t) · E · (1-fc); feF(t) = 1 - feE(t)
Zur Bestimmung der Anfangsgrößen und der Wachstumsziffer der Erdbevölkerung sowie zur Abschätzung der Binde-Faktoren gilt das oben Gesagte, wobei aber im Fall A die Größe feE = 13% sich aus den Zahlen des Jahres 2005 erschließtund im Fall B die lineare Zeit-Funktion feE(t) = feE(t-1)*(1+p) fiktiv angenommen sind. Sie hängen sehr stark von politischen Entscheidungen ab. Die hier angenommene Funktion feE(t) bewirkt, dass in etwa 50 Jahren alle umgewandelte Energie aus erneuerbaren Energien stammt. |
| |
|
|
| Programmiert die Zustands- und Modellgleichungen und simuliert das konstruierte Modell. |
|
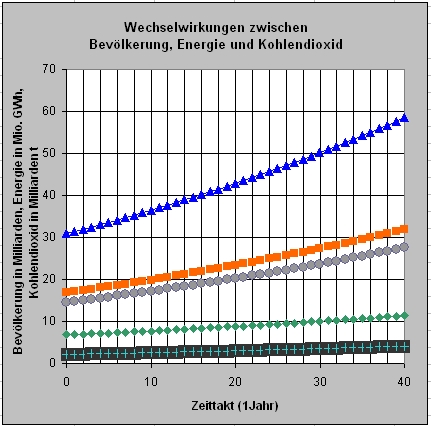
Die programmierte Tabelle für den Fall A und auch ein Simulationsergebnis siehe:
ExcelDateien/Mappe1558nc.htm (nur zur Ansicht) oder ExcelDateien/Mappe1558nc.xls (herunterladbar und interaktiv) |
| |
|
|
blau = Kohlendioxid;
rot = Energie;
grau = fossile Energie
dunkelgrün
= erneuerbare Energie
hellgrün = Bevölkerung
|
|
|
| |
|
|
| |
|
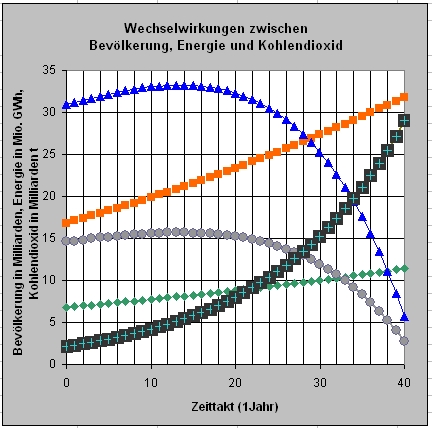
Die programmierte Tabelle für den Fall B und auch ein Simulationsergebnis siehe:
siehe:
ExcelDateien/Mappe1558nd.htm (nur zur Ansicht) oder ExcelDateien/Mappe1558nd.xls (herunterladbar und interaktiv) |
| |
|
|
blau = Kohlendioxid;
rot = Energie;
grau = fossile Energie
dunkelgrün = erneuerbare Energie
hellgrün = Bevölkerung |
|
|
| |
|
|
| |
|
Weitere Simulationen lassen erkennen, dass die Faktoren fc und feE sowie die lineare Funktion und feE(t) auf eine Abnahme bzw. Reduktion des CO2-Gehaltes in der Atmosphäre am stärksten wirken. |
| |
|
|
| Beschreibt das Verhalten des Modells, interpretiert es und beschreibt den Zweck und die Grenzen dieses Modells. |
|
In diesem Modell steigt wie zuvor mit wachsender Bevölkerungszahl auch die Nachfrage nach Energie (rote Kurve). Im Fall B nimmt aber die fossile Energie“kurve“ (graue Kurve) stark ab und nähert sich in den nächsten 50 Jahren dem Wert Null. Weil der Anteil an fossiler Energie an der umgewandelten Energie aber abnimmt , also immer mehr fossile durch erneuerbare Energien (dunkelgrüne Kurve) ersetzt werden, nimmt die Belastung der Atmosphäre mit Kohlendioxid (blaue Kurve) ab. Das zeigt das zweite Diagramm zum Fall B in besonderer Weise recht deutlich.
Zwar wächst der Ausstoß von Kohlendioxid in die Atmosphäre immer weniger, aber er stabilisiert sich auf einem viel zu hohen Niveau, das nicht dem natürlichen Kreislauf des Kohlendioxids (ma0554.htm). entspricht.
Die Verhaltensbeschreibungen der beiden zuvor diskutierten Modelle enden in qualitativen Einsichten. Und das war der Zweck dieser Modelle. Die Simulationsergebnisse vermitteln aber auch neue, weiterführende Fragen:
- Wie lässt sich der Kohlendioxid-Gehalt in der Atmosphäre, der stark mitverantwortlich für die Temperaturerhöhung auf der Erde ist, wieder auf ein natürliches Maß reduzieren? Hierzu siehe in MMM die Szenarien auf der Seite ma0556a.htm.
- Lassen sich mit erweiterten Modellen auch qualitative Zukunftsaussagen in der Weise gewinnen, dass begründeter gesagt werden kann, wenn "heute" nichts passiert, dann haben unsere Kinder und Enkel ein großes Problem?
Mit diesen beiden Fragen zeigen sich wieder die Grenzen der beiden zuvor diskutierten Modelle. Die Modelle müssten erneut erweitert werden. Sie könnten jedoch selbstständig weiterentwickelt werden, so dass eine Reduktion des Kohlendioxids in der Atmosphäre durch eine Erhöhung von Photosynthese oder Bindung in das Modell eingebracht würden. Die Modelle könnten aber auch selbstständig, experimentierend so weiterentwickelt werden. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |



















