|
|
Wir untersuchen, wie schnell
sich
ein grippaler Infekt ausbreitet
und wie er wieder abklingt
|

|
|

|
|

|
|

|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mögliche Anforderungen für das 3. bis
5. Schuljahr |
| |
 |
|
Wir untersuchen (analysieren)
wie schnell sich eine
Erkältung ausbreitet?
|
|
Nehmt einmal an, dass jedes infizierte Kind täglich
jeweils zwei weitere infiziert (Ansteckungszahl)
und die Inkubationszeit
zunächst Null Tage beträgt. Anders gesprochen:
Die neu Infizierten werden sofort krank. Dann
könnt ihr u.a. Folgendes überlegen und
rechnen:
- Wie viel Kinder der Klasse/der Schule sind
nach 2, 3, 4, ... Tagen infiziert?
- Zeichnet die Ausbreitung der Erkältung
so, wie sie unten mit "Köpfen"
begonnen wurde!
- Schätzt einmal, wie lange es dauert,
bis alle Kinder der Schule krank sein können.
- Bei wie viel Kindern der Klasse/der Schule
ist nach 2, 3, 4, ... Tagen die Erkältung
akut, wenn die Inkubationszeit 1 Tag (oder 2
Tage) beträgt? Anders gefragt: wie viel
Kinder sind nach 2, 3, 4, ... Tagen krank, wenn
die jeweils neu Infizierten erst nach einem
Tag (oder zwei Tagen) krank werden?
- Erstellt dazu auch eine passende Tabelle
und rechnet. Berechnet die Zeit, wann alle Kinder
der Schule krank sein können.
- Warum wird bei diesen Darstellungen und Rechnungen
von einem idealen Modell gesprochen?
- Wie könnt ihr euch die Inkubationszeit
mit einem Modell der Vervielfältigung
von Viren erklären?
|
 |
|
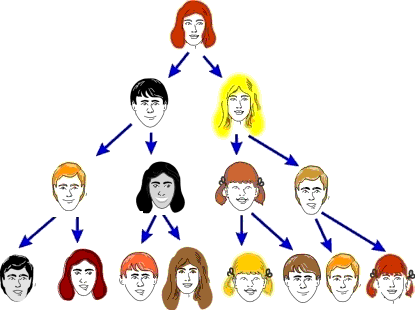
Ein Beispiel für
ein ideales Modell:
Claire infiziert ihren Bruder
Simon und ihre Freundin Sindy.
Simon infiziert seinen Bruder Tom und dessen Freundin
Derya.
Sindy infiziert ihre Schwester Sybille und ihren
Freund Paul.
usw. usw. usw.
|
|
 |
| |
|
|
|
|
 |
|
Gibt es bei infektiösen
Krankheiten auch Todesfälle. Nehmen sie etwa
zu? ...
|
|
Mit den Sachinformationen sind euch auch "Zahlen"
zu Todesfällen in Folge infektiöser
Erkrankungen (Datensätze)
gegeben.
- Seht euch einmal die Zahl der Todesfälle
bei infektiösen Krankheiten in den Jahren
1999 bis 2003 an. Was fällt euch dabei
auf?
- Stellt die Zahlen in Form von Balken dar.
Was fällt euch auf?
- Seht euch zusätzlich die Zahlen an, die
nach Altergruppen aufgeteilt sind, und stellt
sie in Balken dar. Welche Folgerung könnt
ihr aus diesem Balkendiagramm ziehen? Gehen
Oma und Opa etwa nicht zur Grippeimpfung?
- Stellt die Zahlen der an Grippe Verstorbenen
in den Jahre 1955 bis 1970 in Balken dar. Beschreibt
mit Worten, wie sich die Balkenlänge ändert.
Was sagt euch dieses Balken-Diagramm?
- Erstellt zu euren Ergebnissen und Einsichten eine Präsentation.
|
| |
|
Mögliche Anforderungen für das 5. bis
7. Schuljahr |
| |
 |
|
Wie verläuft die
Ansteckungs- und Abklingphase einer Erkältung?
|
|
Nehmt wie zuvor an, dass jedes infizierte Kind
täglich jeweils zwei weitere infiziert (Ansteckungszahl)
und die Inkubationszeit
0 Tage beträgt. Berücksichtigt zusätzlich,
dass die Erkältung nach 7 Tagen abgeklungen
ist. Anders formuliert: Nehmt an, dass die vor
7 Tagen infizierten Kinder niemand mehr anstecken
können. Dann könnt ihr u.a. Folgendes
überlegen und rechnen:
- Wie viel Kinder der Klasse/der Schule sind
nach 2, 3, 4, 5, ... Tagen erkältet? Wie
verläuft die Ansteckungsphase?
- Wie viel Kinder "husten" noch nach
7, 8, 9, 10, ... Tagen? Wie verläuft die
Abklingphase einer Erkältung?
- Erstellt dazu eine passende Tabelle und rechnet.
- Erstellt dazu ebenfalls ein passendes Diagramm.
- Warum wird auch bei diesen Rechnungen noch
von einem idealen Modell gesprochen?
- Erstellt zu euren Ergebnissen und Einsichten eine Präsentation.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
© Pädagogisches Institut für die deutsche Sprachgruppe Bozen 2000 -
.
Letzte Änderung: 06.10.2008
|
 |
|
|
|
|
Mathe-Hilfen
zur Untersuchung
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
| |
|
Mögliche Hilfen
für die
Klassenstufen 3 bis 5
|
| |
| |
| |
|
|
| |
| |
|
|
| |
| |
|
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
| |
| |
|
|
| |
| |
| |
| |
| |
| |
|
Mögliche Hilfen
für die
Klassenstufen 5 bis 7
|
| |
| |
| |
|
|
| |
| |
|
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|



















