Anforderungen /
Aufgaben
|
|
Mögliche "Lösungen" der Anforderung
bezogen auf die Klassen 10 bis 12 |
| |
|
|
Hinweise:
Die Bearbeitung der folgenden Aufgaben kann Teil einer Gesamtlösung von mehreren arbeitsteilig arbeitenden Kleingruppen.
Beschreibung der erwerbaren inhaltlichen und allgemeinen mathematischen Kompetenzen bei der Arbeit an den folgenden Aufgaben |
|
Die folgende Lösung zur Konstruktion und Simulation dynamischer Wechselwirkungen zwischen Bevölkerung, Nahrungsproduktion und Kapital in der Subsahara-Zone kann in einer Teilgruppe der Klasse erarbeitet werden. Sie kann/sollte aber auch Teil einer Gesamtlösung sein, bei der andere Kleingruppen der Klasse an den folgenden komplexen Teilproblemen arbeiten:
Nach der Präsentation der Gruppenlösungen in der Klasse werden gemeinsam Folgerungen erarbeitet und diskutiert.
Für die Erarbeitung der nachfolgenden Lösung und deren Formulierung sind etwa 4 Schulstunden notwendig, wenn Teile dieser Arbeiten auch als Hausarbeit angefertigt werden. Für die Besprechung aller Analysen in der Klasse sind dann noch einmal ca. 2 Schulstunden notwendig. |
| |
|
|
|
|
|
|
|
Konstruktion und Simulation
dynamischer Wechselwirkungen
zwischen
Bevölkerung, Nahrungsproduktion und Kapital |
| |
|
|
| Diskutiert miteinander die komplexen, dynamischen Wechselwirkungen zwischen Bevölkerung, Nahrungsproduktion und Kapitaleinsatz. |
|
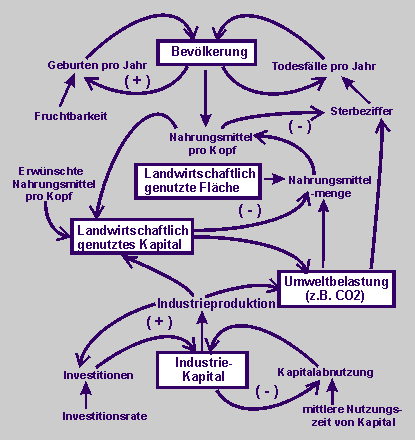
Das folgende komplexe Wirkungsdiagramm ist dem Bericht an den Club of Rome "Die Grenzen des Wachstums (S 83)" entnommen. Es zeigt die Teilstruktur von "Bevölkerung, Kapital und Landwirtschaft in einem noch komplexeren Zusammenhang. |
| |
|
 |
| |
|
|
| |
|
Aber die Subsysteme Bevölkerung, Nahrungsproduktion und Kapital sind bereits an anderer Stelle ausführlich diskutiert und dynamisch modelliert worden. Auf diese Konstruktionen und Simulationen wird hier zunächst verwiesen:
|
|
|
|
Setzt das komplexe Wirkungsdiagramm aus den drei bisher getrennt untersuchten Subsystemen Bevölkerungswachstum, Wachstum der Nahrungsproduktion und Wachstum des Kapitals zu einem zusammen.
|
|
 |
| |
|
|
| Zum Begriff "Wachstumsziffer" siehe "Wachstumszahlen, -Ziffern und -Raten sowie u.a. Arbeitslosen-Quoten" |
|
Es gibt die Zustandsgröße "Bevölkerung (B)". Auf diese wirken zwei Flussgrößen. Die Zunahme_Bevölkerung (Z_B) ist eine positive und die Abnahme_Bevölkerung (A_B) eine negative Rückkopplung. Geburtenrate und Sterberate wirken ihrerseits auf die Flussgrößen. Fruchtbarkeit und Sterbeziffer werden hier nicht betrachtet. |
| |
|
|
| |
|
 |
| |
|
|
| |
|
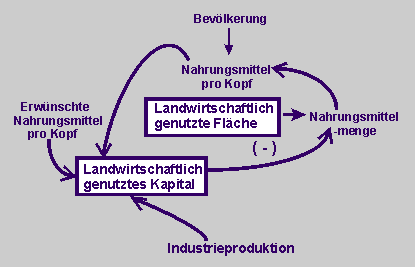
Zustandsgrößen (oder Bestandsgrößen) sind das "Landwirtschaftlich genutzte Kapital (LK)", die "Landwirtschaftlich genutzte Fläche (F)" und die "Nahrungsmittelmenge bzw. die "Nahrungsmittelproduktion (NP)". Diese Bestandsgrößen haben jeweils einen Zuwachs: Mit dem eingesetzten Kapital wächst die nutzbare Fläche und mit der nutzbaren Fläche wächst die produzierte Nahrungsmenge. Entsprechend gibt es also die drei folgenden Flussgrößen Zunahme_Landwirtschaftliches Kapital (Z_LK), Zunahme_Landwirtschaftlich genutzte Fläche (Z_F) und Zunahme_Nahrungsmittelproduktion (Z_NP), auf die jeweils ein Anpassungsfaktor f1, f2 und f3 wirkt, auch um die Dimensionen der Größen aneinander anzupassen.
Die wirkliche Nahrungsmenge pro Kopf (nk) und die erwünschte Nahrungsmenge pro Kopf (enk) erzeugen einen Rückkopplungskreis über das eingesetzte Kapital. |
| |
|
|
| |
|
 |
| |
|
|
| Zum Begriff "Wachstumsziffer" siehe "Wachstumszahlen, -Ziffern und -Raten sowie u.a. Arbeitslosen-Quoten" |
|
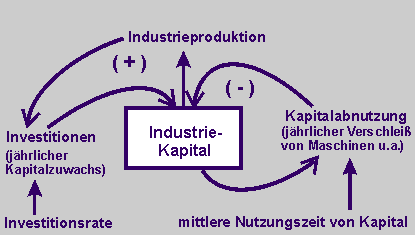
Es gibt die Zustandsgröße "Kapital (K)". Auf dieses wirken zwei Flussgrößen (In) und Ka. Ein Bruchteil des Kapitals wird zur Industrieproduktion Ip genutzt und ein Teil davon für die landwirtschaftliche Produktion. Auf die Flussgrößen wirken einerseits eine Investitionsrate (ir) und andererseits ein Abnutzungsfaktor f. |
|
|
|
| Setzt das komplexe Flussdiagramm ebenfalls aus den drei Flussdiagrammen der bisher getrennt untersuchten Subsysteme Bevölkerung, Nahrungsproduktion und Kapital zu einem zusammen. |
|
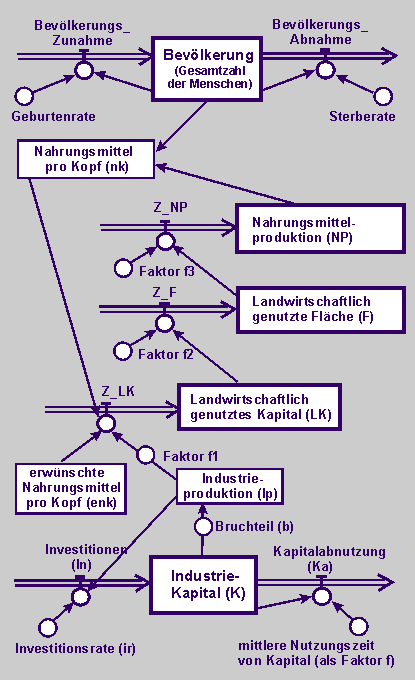
Die drei Wirkungsnetze zu verschiedenen Subsystemen führen wir in eins zusammen und übertragen es dann in das folgende Flussdiagramm. Natürlich müssen die Raten und Faktoren auf das zu untersuchende Gebiet der Welt, nämlich auf die Subsahara-Zone, zugeschnitten werden. Auch das ist nicht ganz einfach und macht analysierende Teiluntersuchungen sowie Recherchen notwendig. Dies z.B. für die Sterbe- und Geburtenraten und auch für die Kapitalentwicklung. |
| |
|
|
|
|
|
|
|
|
Beschreibt das Modell mit Zustands- und Modellgleichungen.
Der Hungerreport 2005 von
"Brot für die Welt" spricht von Hunger, wenn die tägliche Energieaufnahme zwischen
1.400 und 1.800 Kilokalorien
pro Kopf pro Tag liegt.
Normal braucht ein Mensch rund 3000 kcal pro Tag. Das ist die Zielgröße in der folgenden Simulation.
enk = 0,26 Tonnen Weizen pro Jahr pro Kopf entsprechen 0,72 kg pro Kopf pro Tag. Diese Menge entspricht rund 3000 kcal pro Kopf pro Tag,
bei 1g Kohlenhydrate = 4,2 kcal.
Eine Nahrungsproduktion von
100 Millionen Tonnen (Weizen etc.) pro Jahr entsprechen rund
1500 kcal pro Kopf pro Tag.
(Das ist die gelbe Linie in der folgenden Simulation).
Hierzu siehe: ma0334a.htm#Situation
|
|
Die folgenden Zustands- und Modellgleichungen entwickeln wir aus dem vorstehenden Flussdiagramm unter Berücksichtigung eines Zeittaktes zwischen Zustand_neu und Zustand_alt. Alle Anfangsgrößen und Koeffizienten belegen wir mit Zahlen.
B_neu <-- B_alt + Δt · (Z_B - A_B)
Anfangsgröße Bevölkerung B = 750 Millionen
(Subsahara-Zone);
Δt = 1; (Interpretation: Zeittakt = 1 Jahr)
Z_B = B · gr Λ A_B = b · sr
gr = 0,041 Λ sr = 0,029 (Mittelwerte Subsahara-Zone)
*************************************************************
LK_neu <-- LK_alt + Δt · Z_LK
Anfangsgröße landwirtschaftlich genutztes Kapital
LK = 600 Milliarden €;
F_neu <-- F_alt + Δt · Z_F
Anfangsgröße landwirtschaftlich genutzte Fläche
F = 300 Tausend ha;
NP_neu <-- NP_alt + Δt · Z_NP
Anfangsgröße Nahrungsproduktionsmenge
NP = 100 Mill. Tonnen;
Δt = 1 (Zeittakt = 1 Jahr)
Z_LK = (enk - nk) · f1 Λ F = LK · f2 Λ
Z_NP = F · f3 Λ nk = NP/B
enk = 0,26 Tonnen pro Jahr pro Kopf Λ
f1 = 8 Λ f2 = 0,016 Λ f3 = 0,015
***********************************************************
K_neu <-- K_alt + Δt · (In - Ka)
Anfangsgröße Kapital K = 2 Billionen €; Δt = 1; (Zeittakt = 1 Jahr)
In = Ip · ir Λ Ip = K · b Λ Ka = K · f
ir = 0,2 Λ b = 0,4 Λ f = 0,02
|
| |
|
|
| Programmiert das Modell mit Excel. |
|
Wir programmieren zunächst nur die vier Zustandsgleichungen für Bevölkerung, landwirtschaftlich genutztes Kapital, landwirtschaftlich genutzte Fläche und Nahrungsproduktionsmenge sowie die zugehörigen Modellgleichungen. Die Zahlen sind auf eine oder drei Stellen hinter dem Komma gerundet.
Die Faktoren f1, f2 und f3 sind experimentell so ermittelt, dass die verfügbare Nahrungsmenge pro Kopf steigt und sich aus der "Hungerzone" entfernt. Das ist die gewünsche Entwicklung in dieser Weltrregion.
Die Ausgangsgrößen entsprechen in etwa dem Zustand in der Subsahara-Zone (die insgesamt aus 48 Staaten besteht). Die Geburten- und Sterberate sind ein Mittelwert aus einigen dieser Länder und erzeugen eine Bevölkerungszahl, wie sie für 2020 in etwa von der Weltbank eingeschätzt wird.
In einer weiteren Programmierung könnte auch noch das Kapital einbezogen werden. Dies kann und sollte selbsorganisiert geschehen.
Siehe hierzu:
ExcelDateien/Mappe1328a.htm (nur zur Ansicht) oder ExcelDateien/Mappe1328a.xls (herunterladbar und interaktiv)
|
|
|
|
| Simuliert das Modell. |
|
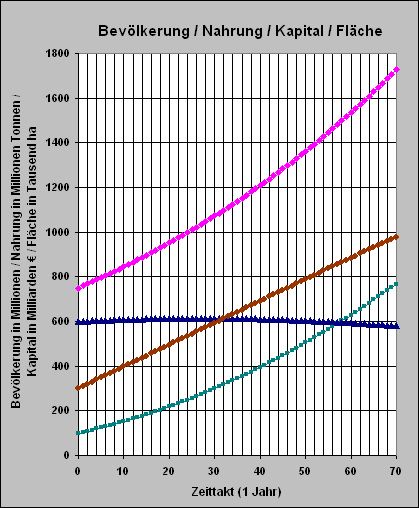
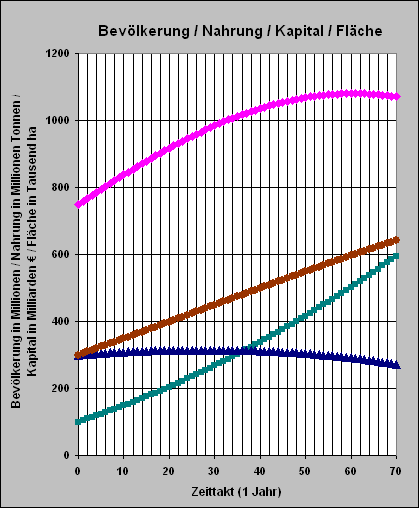
Das folgende Simulationsergebnis entspricht den eingegebenen Größen.
Das folgende Diagramm zeigt also eine agrarbasierte Wachstumsstrategie, da in der Subsahara-Zone die Landwirtschaft der Schlüsselsektor für die volkswirtschaftliche Entwicklung und für die Reduzierung des Hungers ist. Er könnte noch schneller durch höheren Kapitaleinsatz reduziert werden.
|
| |
|
|
Bevölkerung = violett
Kapital = blau
Land = braun
Nahrungsproduktion = grün
|
|
 |
| |
|
|
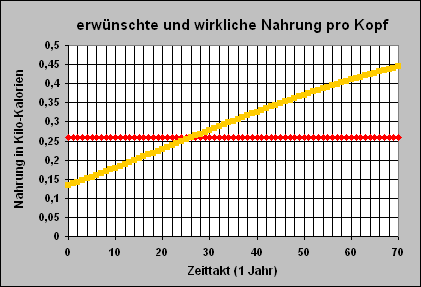
Die wirkliche
Nahrungsmenge
pro Kopf
pro Tag ist gelb
eingezeichnet
Rot ist die erwünschte Nahrungsmenge
von 3000 kcal pro Tag
gezeichnet,
die den Hunger beseitigt.
|
|
 |
| |
|
|
| |
|
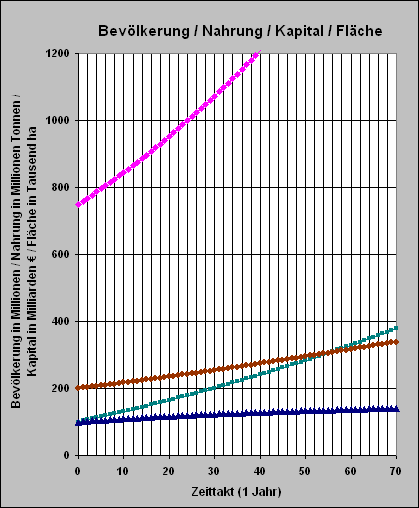
In einer weiteren Simulationen werden die derzeitig vorherrschenden Verhältnisse simuliert, die zur Zeit noch durch eine starke Unterkapitalisierung bzw. durch land grabbing gekennzeichnet sind. Daher wird auf Grund von "bürgerkriegsartigen Querelen" in vielen dieser Staaten in der folgenden Simulation LK = 100 und F = 200 gesetzt. Dann nimmt die Bevölkerung zwar auch weiter zu, aber der Hunger (die gelbe Linie) bleibt noch für sehr lange Zeit weit unter dem notwendigen Nahrungsbedarf von 3000 kcal pro Tag pro Kopf ! |
| |
|
|
| |
|
Siehe hierzu:
ExcelDateien/Mappe1328b.htm (nur zur Ansicht) oder ExcelDateien/Mappe1328b.xls (herunterladbar und interaktiv)
|
| |
|
|
Bevölkerung = violett
Kapital = blau
Land = braun
Nahrungsproduktion = grün |
|
 |
| |
|
|
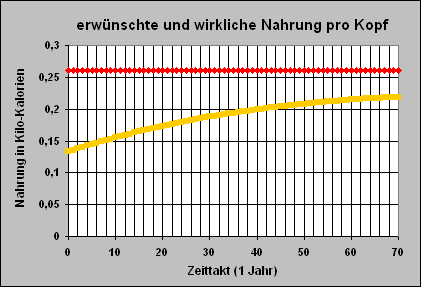
Die wirkliche
Nahrungsmenge
pro Kopf
pro Tag ist gelb
eingezeichnet
Rot ist die erwünschte Nahrungsmenge
von 3000 kcal pro Tag
gezeichnet,
die den Hunger beseitigt.
|
|
 |
| |
|
|
| |
|
In einer dritten Simulationen nehmen wir an, dass durch "Aufklärung" die Geburtenrate gr = 0,041 stetig sinkt aber die Sterberate sr = 0,029 sich durch AIDS immer noch weiter erhöht.
gr = -0,0001 · t + 0,041 und sr = 0,0001 · t + 0,029
Dann ergeben sich auch bei schon bei niedrigerem Kapitaleinsatz LK = 300 aber gleich bleibend hoher Fläche F = 300 schon Verhältnisse, die den Hunger langsam beseitigen.
Siehe hierzu:
ExcelDateien/Mappe1328c.htm (nur zur Ansicht) oder ExcelDateien/Mappe1328c.xls (herunterladbar und interaktiv) |
| |
|
|
Bevölkerung = violett
Kapital = blau
Land = braun
Nahrungsproduktion = grün |
|
 |
| |
|
|
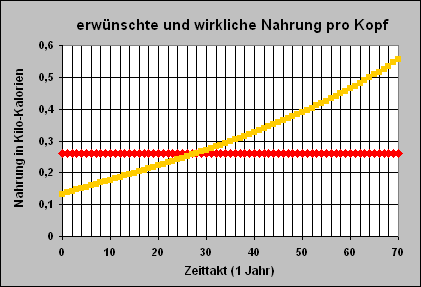
Die wirkliche
Nahrungsmenge
pro Kopf
pro Tag ist gelb
eingezeichnet
Rot ist die erwünschte Nahrungsmenge
von 3000 kcal pro Tag
gezeichnet,
die den Hunger beseitigt. |
|
 |
|
|
|
| Diskutiert den Zweck und die Grenzen der Modells. |
|
Der Zweck dieses Modells ist also alleine eine Formulierung von möglichen Hoffnungen oder Visionen!
Das Modell ist in keiner Weise ein Vorhersagemodell, sei denn die Industrieländer entnehmen den Simulationen den Auftrag, Kapital in die Urbarmachung der Länder zum Zweck einer verbesserten Nahrungsproduktion zu investieren.
Für den Fall eines zunehmenden Grades an Kapitaleinsatz (und damit einer Mechanisierung in der bäuerlichen Landwirtschaft) wird sich die Nahrungssituation - natürlich den länderspezifischen Verhältnissen angepasst - verbessern lassen. Aber die Mechanisierung sollte dabei in erster Linie der Steigerung der Flächenproduktivität, Arbeitserleichterung und Qualitätsverbesserung dienen, nicht aber zur Arbeitskräftefreisetzung führen, weil nur so ländliche Arbeitslosigkeit (und damit erneuter Hunger in diesen Kreisen) vermieden werden kann.
Die Grenzen dieses Modells liegen in den Annahmen, die in dem obigen Flussdiagramm zu sehen sind. Denkbar wären auch noch andere Wechselwirkungs-Kopplungen, in denen z.B. auch noch die Umweltproblematik mit berücksichtigt würde. |
| |
|
|
| Verschriftlicht eure Ergebnisse und erstellt eine Präsentation. |
|
Wesentliche Ergebnisse sind in den ExcelMappen dargestellt. Die Interpretationen sind im vorstehenden Text zu finden. |
| |
|
|
Anmerkung: |
|
Die hier dargestellten "möglichen Lösungen" sind fiktiv.
Sobald Schülerlösungen vorliegen, werden sie unter
exemplarische Schülerarbeiten veröffentlicht. |























