|
Faszinierende Arches, elegante Brücken, kunstvolle Bögen
Abstraktion und Modellierung von Bogenformen in Natur, Technik und Kultur |
|
 |
|
 |
|
 |
|
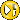 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
 |
|
Double Arch, USA
|
|
Burg Conway, Wales
|
|
Kloster in Barcelona |
| |
Mögliche Anforderungen für die 8. bis 10. Klasse (für Wiederholungen in 11) |
| Nach der fotografischen Wahrnehmung von Bögen entscheidet euch für die Arbeit an einem Bogen. Modelliert den Bogen und diskutiert eure Ergebnisse in der Klasse ! |
| |
|
|
|
|
 |
|
Wahrnehmung von unterschiedlichen Bogen-Formen
|
|
Beim Betrachten
der Bögen im "Ausstellungsraum" werdet ihr sicher dazu angeregt, auch in eurer Umgebung eine Vielfalt von ganz
unterschiedlichen Bogen-Formen "bewundern" zu können.
- Fotografiert (digital) einige dieser Bögen (in der Natur, an und in Gebäuden oder an Brücken) und stellt sie in eurer Klasse oder auch in der Galerie dieser Lernumgebung aus.
|
|

|
|
Modellierung
von realen Bogen- Formen durch "geometrische" Abstraktionen
|
|
- Entscheidet euch in eurer Kleingruppe für einen Bogen, an dem ihr weiter arbeiten wollt.
- Abstrahiert die Bogenform von dem digitalen Foto des Bogens indem ihr (u.a. mit einem Computer-Zeichenprogramm) die Form nachzeichnet (ggf. mit ihren Besonderheiten wie Aufhängungen und Straßenverlauf bei Brücken). Vergrößert ggf. das Bild auf etwa DIN A4 Größe.
- Beschreibt die Bogenform in ihren Hauptmerkmalen (Konstruktion, Material und/oder Geometrie).
- Druckt das abstrahierte Bild des Bogens aus, legt durchscheinendes Millimeterpapier darüber und paust die
Form des Bogens ab.
- Korrigiert
beim Abpausen die perspektivische Verzerrung, die in der Fotografie stecken kann, so gut es geht, etwa durch "gedankliches
Drehen" des Bildes.
|
 |
|
Modellierung
von realen Bogen- Formen durch funktionale Beschreibung
|
|
- Zeichnet in
die abgepausten Bogenbilder ein Koordinatensystem so ein, dass ihr
die Koordinaten von markanten Punkten des Bogens gut ablesen könnt.
- Schreibt die
Koordinaten einiger Punkte in eine Wertetabelle.
- Findet
den Term, der den Verlauf des Bogens (Graphen) gut beschreibt.
- Nutzt bei
euren Arbeiten ggf. ein Tabellenkalkulationsprogramm (Excel) oder ein Computer-Algebra-Programm (Derive).
- Verschriftlicht eure Ergebnisse und erstellt eine Präsentation.
|
 |
|
Berechnungen
an Brücken-Bögen
mit Hilfe der gefundenen Terme
Diese Anforderung stellt höhere Ansprüche an euch.
|
|
- Findet die Funktionsgleichung des Bogens der Müngstener Brücke oder der Autobahnbrücke über die A1.
- Findet ebenfalls die Funktionsgleichung für die Eisenbahnlinie oder die Straße, die über die Brücke führt.
- Findet eine Funktionsgleichung für den Verlauf des Talhanges bzw. der Böschung.
- Berechnet mit Hilfe der gefundenen Funktionen die Länge einzelner Streben oder besonderer Schnittpunkte.
- Berechnet die
Bogenhöhe und die Spannweite der Brücke.
- Berechnet selbstorganisiert weitere Größen an den beiden oder einer der Brücken.
- Verschriftlicht eure Ergebnisse und erstellt eine Präsentation.
|
|
|
|
|
|
|
|
|
|
Letzte Änderung: 25.03.2009
© Pädagogisches Institut für die deutsche Sprachgruppe
- Bozen. 2000 -
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
| |
 |
Buro Creek Bridge, Arizona |
| |
| |
| |
| |
| |
Zur Bearbeitung der Anforderungen (Aufgaben)
gibt es für euch die folgenden mathematischen Hilfen
(blau unterlegt)
und Werkzeughilfen
(grün unterlegt): |
| |
|
Mögliche Hilfen für die
Klassenstufen 8 bis 10 |
|
| |
|
|
| |
|
|
|
|
| |
|
|
|
| |
|
|
|
|
|
|
|
|