|
|
|
am Beispiel
des realen Problems
|
|
Beschreibung des Unterrichtsverlaufs
1. UStd:
Diskussionen zum realen Problem sowie Wahrnehmung der Sachinformationen zum realen Problem
2. UStd:
Entwicklung von Fragen durch Diskussion des realen Problems;
Sammlung der Fragen, die Schülerinnen und Schüler bearbeiten möchten;
Entscheidung der Schülerinnen und Schüler für die Bearbeitung eines Fragenbereiches;
Bildung von "interessengleichen" Kleingruppen auf der Basis der Entscheidungen
3. bis 6. UStd:
Mathematische Modellierungsarbeiten an den
selbst gewählten Fragen in "interessengleichen" Kleingruppen;
sachangemessene und kontextbezogene
Interpretation der Ergebnisse der
mathematischen Modellierung;
Erstellung einer Präsentation
7. und 8. UStd:
Präsentation der Kleingruppen-Ergebnisse in der Klasse und Diskussion der Ergebnisse im Sachzusammenhang des realen Problems
9. und 10. UStd:
Systematisierung
der zur Modellierung genutzten Mathematik; in diesem Fall Einführung der Exponentialfunktion
11. und weitere UStd:
Übungen und Anwendungen zu exponentiellen Funktionen
in anderen Wirklichkeits-Kontexten
|
| |
|
|
|
|
|
1. Unterrichtsstunde:
Diskussionen zum
realen Problem
sowie Wahrnehmung der Sachinformationen zum Problem (in der Klasse und dann in spontan gebildeten Kleingruppen)
|
|
 |
| |
|
|
Arbeitsauftrag / Arbeitsauträge |
|
Die Lehrerin oder der Lehrer führt in eine Diskussion des realen Problems ein. Dabei verweist sie/er die Schülerinnen und Schüler auch auf die aufbereiteten Sachinformationen zu diesem realen Problem. Sodann erteilt sie/er folgende Arbeitsaufträge:
- Setzt die begonnene Diskussion in spontan gebildeten Kleingruppen fort, notiert das für euch Wichtige. Lasst euch in euren Diskussionen unterstützen durch:
a) eine mögliche Bild-Diskussion oder durch eine fast unglaubliche Geschichte zum Thema
b) kurze Blicke auf die Problemlage viröser Epidemien und Pandemien.
- Legt ein Projektheft (eine Projektmappe) an, in dem ihr alle benutzen "Arbeitsblätter" abheftet und alle weiteren Ergebnisse aufschreibt. Notiert auch, was euch im Verlauf des Unterrichts insbesondere betroffen macht, was euch gefallen oder nicht gefallen hat sowie das, was euch Schwierigkeiten im Verständnis bereitet hat.
|
| |
|
|
Didaktische, methodische und organisatorische Anregungen: |
|
Die Seiten (Bilddiskussion und Blicke auf...) können als "Arbeitsblätter" ausgedruckt werden. Schülerinnen und Schüler können dann das für sie Wichtige unterstreichen oder hervorheben. Die Seiten können aber auch am Computer gelesen werden. Dann erfolgen die Notizen im Projektheft oder in den selbst ausgedruckten Seiten. Auf diese Weise können und sollen die persönlichen Interessen zur Bearbeitung einer bestimmten Frage geweckt werden.
Diese Eingangdiskussion sollte in jedem Fall stattfinden, damit erstens die späteren mathematischen Modellierungsarbeiten im Problemkontext interpretiert und zweitens auch die Diskussionen nach den Kleingruppen-Präsentationen durch die Jugendlichen in einem Problemzusammenhang geführt werden können.
Die Formalisierungen zur Exponentialfunktion erfolgen erst in der neunten Unterrichtsstunde. Das ist für Mathematiklehrerinnen und -lehrer ungewohnt. Aber: Die Systematisierungen zur Exponetialfunktionen erfolgen dann so, dass zuvor bereits Wertetafeln und Grafen selbstreguliert bei der Modellierung genutzt worden sind. Vor der Systematisierung und Formalisierung haben die Schülerinnen und Schüler bereits die Erfahrung gemacht, dass diese Darstellungsform einen Zweck hat. Sie dient dem Erkenntnisgewinn in realen Zusammenhängen, der handlungsleitende (emanzipatorische) Ziele verfolgt.
Die "Anwendungssituation" dient also nicht nur dazu (wie es häufig in Schulbüchern geschieht) für eine kurze Zeit zu motivieren. |
| |
|
|
|
|
|
2. Unterrichtsstunde:
Entwicklung von Fragen durch
Diskussion des realen Problems |
|
 |
| |
|
|
Arbeitsauftrag / Arbeitsauträge |
|
In den Kleingruppen, die sich spontan in der ersten Unterrichtsstunde gebildet haben, wird die begonnene Diskussion für etwa 25 Minuten fortgesetzt, etwa mit dem Arbeitsauftrag:
- Diskutiert miteinander, welche Fragen sich bei diesem realen Problem ergeben und schreibt dann diejenigen Fragen auf, die euch ganz persönlich interessieren. Lasst euch unterstützen durch die Seite: Wie breitet sich u.a. das HI Virus aus? Mit welcher Geschwindigkeit? Und mit welcher Dynamik? ...?
|
| |
|
|
Didaktische, methodische und organisatorische Anregungen: |
|
Auch diese Seite kann als "Arbeitsbogen" ausgedruckt und genutzt werden. Die Seite kann aber auch am Computer gelesen werden. Dann müssen die persönlich interessierenden Fragen im Projektheft notiert werden. |
| |
|
|
|
|
|
Noch 2. Unterrichtsstunde:
Sammlung der Fragen, die Schülerinnen und Schüler bearbeiten möchten
Entscheidung der Schülerinnen und Schüler für die Bearbeitung eines Fragenbereiches
Bildung von "interessengleichen" Kleingruppen auf der Basis der Entscheidungen |
|
 |
| |
|
|
Didaktische, methodische und organisatorische Anregungen: |
|
Die Lehrkraft bündelt die Fragen zu Bereichen, bereitet die Entscheidung der Schülerinnen und Schüler für die Arbeit an einem dieser Fragebereiche vor und organisiert auf dieser Basis quasi "interessengleiche" Kleingruppen. Möglich ist aber auch eine Binnendifferenzierung nach Leistung.
Die Lehrperson möchte aber in jedem Fall erreichen, dass mindestens einige Kleingruppen an den beiden folgenden Analysen arbeiten:
Denn diese beiden Analysen geben in der später folgenden Systematisierungsphase den Anlass, auch Exponentialfunktion zu formalisieren. Hier ist also Beratungsaufwand durch die Lehrperson notwendig.
[Soll die funtionale Modellierung mit der dynamischen verglichen werden, so sollte auch eine Kleingruppe arbeiten an einer
|
| |
|
|
|
|
|
3. bis 6. Unterrichtsstunde:
Mathematische Modellierungsarbeiten an den selbst gewählten Fragen
in "interessengleichen" Kleingruppen
Sachangemessene
und kontextbezogene Interpretation der Ergebnisse der mathematischen Modellierung
Erstellung einer Präsentation
|
|
 |
| |
|
|
Arbeitsauftrag / Arbeitsauträge |
|
Die "interessengleichen" Kleingruppen erhalten nun die folgenden Arbeitsaufträge:
- Arbeitet in den nächsten vier Mathe-Stunden und auch Zuhause selbstreguliert (d.h. selbstständig, selbstorganisiert und selbstverantwortet) an den Fragen, die ihr zuvor ausgewählt habt. Für euch passende Anforderungen finden ihr unter:
Kleingruppe(n) 1: Analyse der epidemischen Ausbreitung von AIDS in Deutschland
Kleingruppe(n) 2: Analyse der epidemischen Ausbreitung von AIDS in anderen Ländern der Erde und interpretativer Vergleich der Entwicklungen
[Kleingruppe(n) 3: Konstruktion und Simulation einer Epidemie oder Pandemie]
Auf diesen Seiten, auf denen ihr die Anforderungen findet, findet ihr auch mathematische Hilfen (in der rechten Spalte der Seite) und Hilfen zum Sachverhalt (eingebaut in die Anforderungen).
- Ich werde euch bei eurer Arbeit beobachten (und ggf. bewerten, wie ihr euch in euren Kleingruppen gegenseitig helft und wie ihr miteinander kommuniziert und kooperiert). Wenn ihr aber nach einer eingehenden Beratung in eurer Kleingruppe mit eurer Arbeit nicht mehr weiter kommt, so berate ich euch auf Anfrage hin.
- Stellt eure Modellierungsergebnisse (Arbeitsergebnisse) in euren Projektheften dar. Nutzt dabei die euch bisher bekannte Mathe, (er)findet aber auch neue hinzu.
- Interpretiert die Ergebnisse sachangemessen im Kontext des gesellschaftlich bedeutungsvollen Problems der „weltweiten Ausbreitung von HI-Viren“ und schreibt sie auf.
- Erstellt in eurer Kleingruppe eine Präsentation sowohl für die Modellierungsergebnisse als auch für die Interpretation. Hilfen findet ihr unter "Anregungen zur Präsentation der Arbeitsergebnisse" auf der Eingangsseite des realen Problems.
|
| |
|
|
Didaktische, methodische und organisatorische Anregungen: |
|
Wiederum können die Seiten mit den Anforderungen ausgedruckt werden. Sie können auch nach Word exportiert werden und auf die eigenen Anliegen oder auf die der Kleingruppen hin umgestaltet und neu konfiguriert werden.
Es ist sicher hilfreich, wenn die zuvor beschriebenen Arbeitsaufträge kleingruppenbezogen formuliert und an die Jugendlichen weitergegeben werden. Natürlich können die Kleingruppen 1 bis 3 mehrfach vorkommen.
Sobald aber während der Modellierungsarbeiten bestimmte Datenbestände oder Computer-Werkzeuge gebraucht oder mathematische Hilfen genutzt werden sollen, ist eine Arbeit am Computer notwendig.
Die Lehrkraft sollte sich unbedingt alle anklickbaren Sachinformationen und mathematischen Hilfen zum realen Problem ansehen. Das ist wichtig, um den Kleingruppen, die irgendwo stecken bleiben, Tipps zur selbstregulierten Arbeit geben zu können.
Bei der modellierenden Arbeit werden die Kleingruppen von der Lehrperson „gecoacht“. Es wird ihnen auch dabei geholfen allgemeine (prozessorientierte) Kompetenzen (anzubahnen oder) zu erwerben d.h. u.a.:
- dass Jugendliche ihre Fragen mit der bis dahin bekannten Mathe (sowie der selbstständig hinzu erfundenen Mathe) mathematisch modellieren können,
- dass sie ihre Arbeit selbst organisieren und selbst verantworten (begründen) können,
- dass sie eine ansprechende Präsentation erarbeiten und dann auch halten können (eine Präsentation, die ggf. auch in der Klasse ausgehangen werden kann),
- dass sie Kommunikations- und Kooperationsregeln einhalten können (das ist eine Grundlage der Teamfähigkeit).
Werden die prozessorientierten (oder allgemeinen) mathematischen Kompetenzen bewertet, so sollten die Jugendlichen dies vor ihrer Arbeit wissen.
An dieser Stelle sei darauf verwiesen, dass prozessorientierte Kompetenzen nur in einem komplexeren Arbeits- oder Lern-Prozess angebahnt und gelernt werden können.
Wahrscheinlich muss die Lehrkraft schon ab dem Ende der zweiten selbstregulierten Arbeitsstunde immer wieder darauf hinweisen, dass eine Präsentation vor der Klasse zu halten ist. Und dass die Arbeiten nach der vierten selbstregulierten Arbeitsstunde beendet sein müssen.
Soll diese Präsentation von der Lehrperson bewertet werden, so muss dies vorher mitgeteilt werden.
Während der Modellierungsphase übernimmt die Mathematiklehrerin bwz. der Mathematiklehrer in Sachfragen in der Regel die Rolle eines kompetenten Laien.
Für die Mathematiklehrerin oder den -lehrer kann es bei der Unterrichts-Vorbereitung sehr hilfreich sein, sich die möglichen Lösungen zur:
anzusehen. Die Lösungen zeigen, was von den Schülerinnen und Schülern erwartet werden kann oder sollte. Aber die Lösungen gehen davon aus, dass die Exponentialfunktion und eine dynamische Modellierung bereits bekannt ist. |
| |
|
|
|
|
|
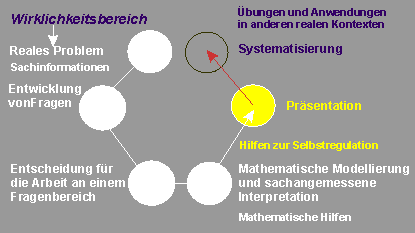
| 7. und 8. Unterrichtsstunde:
Präsentation der Kleingruppen-Ergebnisse in der Klasse und Diskussion der Ergebnisse im Sachzusammenhang des realen Problems
|
|
 |
| |
|
|
Arbeitsauftrag / Arbeitsauträge |
|
Die Lehrkraft stimmt sich mit den Kleingruppen ab, in welcher Reihenfolge die Präsentationen vor der Klasse erfolgen. Dann erteilt sie etwa die folgenden Arbeitsaufträge:
- Jede Kleingruppe stellt ihre Arbeitsergebnisse vor der Klasse so vor, dass alle anderen in der Klasse sie auch verstehen und nachvollziehen können. Also: Lasst immer genügend Zeit, damit die Anderen sich auch Notizen in ihrem Projektheft machen können. Hetzt nicht durch euren Vortrag.
- (Ggf.: Ich habe vor, die Präsentation zu bewerten.)
- Jede Kleingruppe beleuchtet in ihrem Vortrag das weltweite Problem der Ausbreitung von HI-Viren unter einem anderen "Gesichtspunkt". Alle diese hängen aber, wie wir in der Eingangsdiskussion des Problems bereits festgestellt haben, irgendwie miteinander zusammen. Und genau das wollen wir gemeinsam diskutieren, nachdem alle Vorträge gehalten worden sind. So wollen wir erreichen, dass es nicht bei der Summe (Addition) der Einzelbeiträge bleibt, sondern die Diskussion ein neues Ganzes erwirkt.
- In einem abschließenden Gespräch wollen wir auch noch klären, welchen Wert eine arbeitsteilige Arbeit innerhalb eines Teams hat.
|
| |
|
|
Didaktische, methodische und organisatorische Anregungen: |
|
Auch das Präsentieren-Können ist eine wichtige prozessorientierte (allgemeine) mathematische Kompetenz. Die Erstellung kostet Zeit!
Die Jugendlichen sollen durch die Gesamtheit der Präsentationen zur Erkenntnis von Zusammenhängen gelangen, deren Bewertungen für ihr eigenes individuelles und gesellschaftliches Handeln bedeutungsvoll sein können (emanzipatorische Kompetenzen!). Sie können die mathematische Modellierung als eine Erkenntnishilfe zur Bewertung des Problems erleben. Mathe bekommt einen anderen Sinn als nur und lediglich ihren Selbstzweck.
Alle Kleingruppen können bei den Präsentationen erleben, wie die Modellierung ihres Teilbereiches in eine vollständigere Modellierung des realen Problems eingebettet ist.
Die Jugendlichen können so erleben, dass arbeitsteilige Teamarbeit produktiv ist und keine „Zeit“ verschwendet.
Nach diesen 3 Wochen (bei drei Mathestunden pro Woche) sollte in der Regel keine Klassenarbeit geschrieben werden. Zu Beginn der projektorientierten Unterrichtsphase sollte mit den Jugendlichen vereinbart werden, was zur Leistungsbewertung am Ende herangezogen wird (z.B. die Projektmappe, die Präsentation, die Beobachtungen zum Arbeits- und Sozialverhalten ...). Soll aber eine Klassenarbeit geschrieben werden, dann bieten sich nur Aufgaben an, die auch das zuvor Gelernte abprüfen. Solche Aufgaben sind zu finden unter:
|
| |
|
|
|
|
|
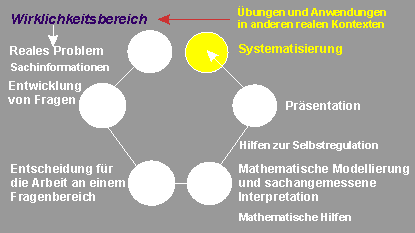
9. und 10. Unterrichtsstunde:
Systematisierung der zur Modellierung genutzten Mathematik; in diesem Fall Einführung der linearen Funktion
11. und weitere Unterrichtsstunden:
Übungen und Anwendungen
der linearen Funktion
in anderen
Wirklichkeits-Kontexten
|
|
 |
| |
|
|
Fragend-entwickelder Unterricht in der Systematisierungsphase zur Einführung der linearen Funktion
|
|
Die Lehrerin oder der Lehrer lenkt den Blick der Schülerinnen und Schüler auf die Präsentationen der Kleingruppen 1 und 2.
In fragend-entwickelnder Form werden dann an den grafischen Darstellungen die Besonderheiten der Exponentialfunktion herausgearbeitet.
|
| |
|
|
Didaktische, methodische und organisatorische Hinweise: |
|
Der Unterricht in der Systematisierungsphase wird fragend-entwickelnd weitergeführt. Entweder kann jetzt das eingeführte Schulbuch genutzt werden oder es können die folgenden Ausarbeitungen genutzt werden:
|
|
|
|
Didaktische, methodische und organisatorische Hinweise zu:
Individuellen Übungen und Anwendungen
der linearen Funktion
in anderen
Wirklichkeits-Kontexten |
|
Für die notwendigen Übungen zu Exponentialfunktionen und zur Anwendung von exponentiellen Funktion in anderen Anwedungskontexten wird insbesondere verwiesen auf:
Im Weiteren wird verwiesen auf:
|
















